Architetture parallele

L’inserimento di un pipelining nell’architettura di un microprocessore tradizionale (SISD) consente di introdurre una sorta di parallelismo nell’organizzazione di un

microprocessore. Infatti, mentre uno stadio provvede ad effettuare le elaborazioni che gli competono riguardo ad un ‘istruzione, lo stadio precedente, rimasto libero, può effettuare le operazioni che gli competono riguardo all’istruzione successiva.

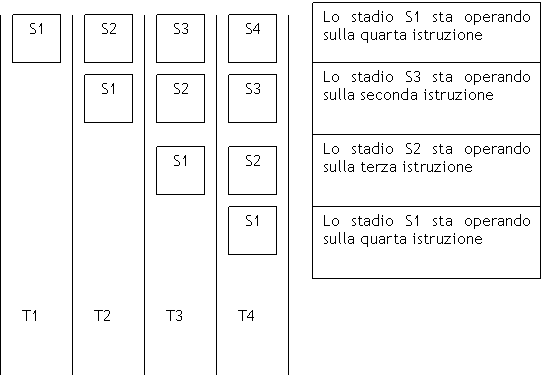
Nella figura abbiamo l’esempio di un pipeline a quattro stadi: dal disegno appare evidente che, fatta eccezione per i tre cicli iniziali necessari a riempire il pipeline, ad ogni ciclo di clock vengono trattate quattro istruzioni alla volta. Stiamo eseguendo in parallelo quattro istruzioni. Questo parallelismo, però, non è perfetto. Osserviamo, infatti, che al ciclo di clock T4 uscirà dal pipeline l’output della prima istruzione, al ciclo T5 emergerà dal pipeline l’output della seconda istruzione e così via. Se il parallelismo fosse perfetto ad ogni ciclo di clock dovrebbe emergere dal pipeline l’output di tutte e quattro le istruzioni. Il parallelismo introdotto dall’architettura pipeline viene detto parallelismo temporale.

Si parla, invece, di parallelismo spaziale quando si hanno più unità di elaborazione che possono eseguire contemporaneamente più istruzioni. Ad ogni ciclo di clock più risultati emergono contemporaneamente dalle unità di esecuzione.

Definizione di parallelismo

Definiamo come massimo grado di parallelismo il numero massimo di bit che il nostro microprocessore può elaborare contemporaneamente durante un ciclo macchina. Se, ad esempio, abbiamo una struttura SIMD con quattro unità di elaborazione ed ogn’una di queste ha una architettura pipeline costituita da 5 stadi, supponendo che tale microprocessore opera su dati lunghi 64 bit, ogni unità elaborerà contemporaneamente un numero di bit pari alla lunghezza dei dati moltiplicato il numero degli stadi del pipeline (che lavorano contemporaneamente su dati diversi)

Poiché abbiamo quattro unità di elaborazione, il parallelismo totale si otterrà moltiplicando il dato precedente per il numero delle unità

Ora questo è il parallelismo massimo poiché non è detto che, ad ogni ciclo di clock, tutte le unità di esecuzione stiano lavorando. Se, ad esempio, si sta eseguendo un’istruzione con operandi scalari e non vettoriali, opera una sola unità di esecuzione. Quindi, ad ogni ciclo di clock, abbiamo un parallelismo

Si può calcolare un parallelismo medio sommando il parallelismo registrato in ogni ciclo di clock e facendone la media sul numero n dei cicli di cicli di clock totali.

Il rapporto fra il parallelismo medio ottenuto negli n cicli di clock e il parallelismo massimo prende il nome di tasso di utilizzo

Il grado massimo di parallelismo si ottiene moltiplicando la lunghezza delle word utilizzate dal microprocessore per la lunghezza del bit slice. Dato un certo numero di parole, si chiama bit slice la stringa di bit che si ottiene estraendo dalle parole tutti i bit che occupano la stessa posizione.

Se riprendiamo l’esempio di prima, consideriamo le parole a 64 bit presenti in tutte le unità di elaborazione, ed estraiamo, ad esempio, tutti i bit che occupano la prima posizione in ogni parola. Poiché abbiamo 5*4=20 parole , otterremmo uno slice costituito da 20 bit. Moltiplicando il bit slice m per la lunghezza n di ogni word abbiamo il numero totale di bit che possono essere elaborati contemporaneamente.

P = n*m

Assenza di cicli in una elaborazione vettoriale.

Un processore scalare, per elaborare dati vettoriali deve procedere attraverso esecuzioni cicliche di operazioni scalari. Ad esempio, per effettuare una somma di due vettori, dovremo eseguire il seguente ciclo

for (i=0;i<n;i++)

{

C[I]= A[I]+ B[I]

}

Una notevole parte del tempo impiegato per eseguire la somma dei due vettori sarà assorbita dalle operazioni di incremento del contatore e di valutazione della condizione di fine ciclo.

Un elaboratore di tipo vettoriale non necessita di cicli e l’esecuzione della somma vettoriale potrà essere effettuata mediante l’esecuzione di una sola istruzione

C[1:n] = A[1:n] + B[1:n]

Se la lunghezza del vettore è minore o pari al numero delle unità di elaborazione , la somma avverrà in un sol colpo

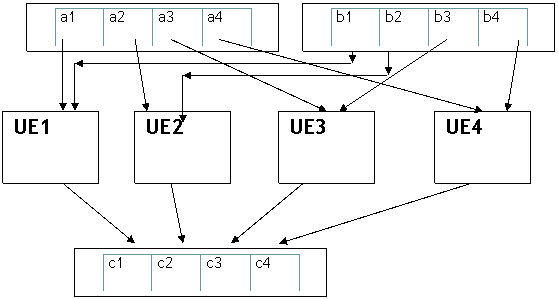
Se, invece, i vettori hanno una lunghezza superiore al numero di unità di elaborazione, l’unità di controllo del microprocessore dovrà suddividere i vettori operandi in blocchi di più scalari e li ripartisce fra le varie unità di esecuzione. In tal caso l’operazione di somma non avverrà in un sol colpo, ma in ogni caso è più veloce di quella di processore scalare soprattutto per il fatto che il controllo dei cicli è affidato all’hardware e non al software.

SIMD: ORGANIZZAZIONE DI BASE

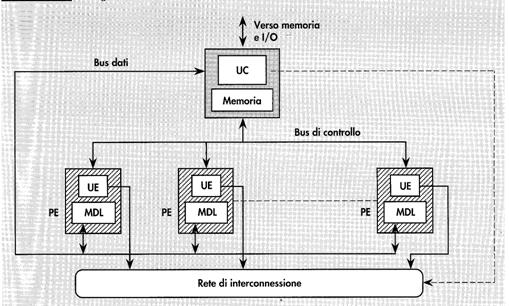
Nella figura seguente abbiamo lo schema dell’organizzazione di un processore vettoriale. In tale struttura, una batteria di elementi di elaborazione, detti Processing Elements PE, agisce sotto la supervisione di un’unica unità di controllo UC. L’Unità di Controllo è l’unica a poter dialogare con la memoria e le unità di IO esterne al processore. I PE sono dotati di un’area locale di memoria detta Memoria dati Locale (MDL), nella quale vengono memorizzati i dati distribuiti dalla unità di controllo. L’unità di controllo contiene anch’essa una memoria locale, le unità di decodifica e controllo vere e proprie, ed, infine, un processore scalare: quando viene effettuato il fetch di un’istruzione vettoriale la UC provvede a suddividere i suoi operandi fra le varie PE affinché queste provvedano ad eseguire l’istruzione; quando viene effettuato il fetch di un’istruzione scalare, essa viene eseguita direttamente dal processore scalare presente nella UC.

Lo scambio delle informazioni tra UC ed elementi di elaborazione avviene tramite gli appositi bus interni.

La rete di interconnessione, anch’essa sotto il controllo della UC, garantisce lo scambio dei dati tra i diversi PE. Infatti, in alcuni algoritmi è utile lo scambio dei dati fra le varie unità. Un possibile esempio è quello del calcolo delle somme parziali degli elementi di un vettore


V(0)	V(1)	V(2)	V(3)
2	3	1	7

Dato il vettore dell’esempio volgiamo effettuare le somme parziali dei suoi singoli elementi. La somma parziale di ordine k sarà data da

per cui

S(0) = V(0) = 2

S(1) = V(0)+V(1) =2+3

S(2) = V(0) +V(1)+V(2) = 2+3+1

S(3) = V(0)+V(1)+V(2)+V(3)=2+3+1+7

Tenendo presente che

S(1) = S(0)+V(1)

S(2) = S(1)+V(2)

S(3) = S(2)+V(3)

Possiamo immaginare il seguente algoritmo:

nel primo passo i componenti del vettore vengono distribuiti fra tutte le PE


PE0	PE1	PE2	PE3
2	3	1	7

Nel secondo passo ogni PE effettua la somma fra il suo dato e quello del PE precedente


PE0	PE1	PE2	PE3
2	3+2=5	1+3=4	7+1=8

Nell’ultimo passo ogni PE effettua la somma fra il suo contenuto e quello del PE che si trova due posizioni prima

PE0

PE1

PE2

PE3

4+2=6

8+5=13

Questo problema è un esempio della possibilità che sia necessario un trasferimento di dati fra i vari PE.

L’UNITA’ DI CONTROLLO

Il compito fondamentale dell’unita’ di controllo e’ quello di prelevare dalla memoria istruzioni e dati, decodificare le istruzioni, eseguire immediatamente istruzioni scalari e di controllo, oppure configurare gli elementi di elaborazione e diffondere i dati per sovrintendere all’esecuzione distribuita di istruzioni vettoriali.

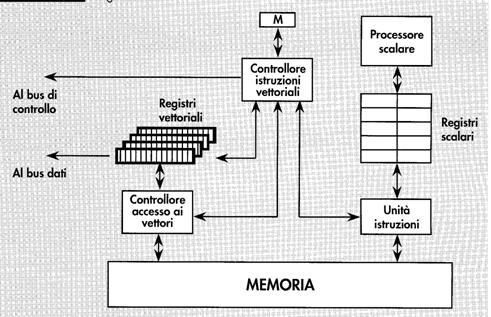
Per realizzare tali funzionalita’, la UC e’ organizzata secondo una architettura:

Il fetch e il riconoscimento delle istruzioni e’ demandato all’Unita’ Istruzioni: la UI e’ responsabile delle istruzioni scalari e di controllo che saranno immediatamente decodificate.

La UI effettuera’ anche l’eventuale fetch degli operandi che saranno inviati al banco dei registri scalari.

Tali istruzioni saranno eseguite dal processore scalare.

Ogniqualvolta l’Unita’ Istruzioni riconosce un’istruzione vettoriale, il monitoraggio della sua esecuzione passa al controllore delle istruzioni vettoriali, che ne iniziera’ la decodifica.

Il successivo compito del CIV e’ il calcolo degli indirizzi effettivi degli operandi vettore, il cui fetch dalla memoria e’ demandato al controllore di accesso ai vettori: dopo aver calcolato tali indirizzi, il CIV dovrà scomporre i vettori nei sottovettori da distribuire ai vari elementi di elaborazione.

Tali insiemi di dati saranno temporaneamente immagazzinati nei registri vettoriali.

Non è detto che tutti i PE siano impegnati nell’esecuzione di un’istruzione: è l’unità di controllo a stabilire quali PE saranno coinvolti nell’esecuzione dell’istruzione.

Sarà ancora il controllore delle istruzioni vettoriali a inviare tramite il bus di controllo i segnali necessari al mascheramento dei PE: a tale scopo viene utilizzato un opportuno registro maschera.

Tutte le unita’ descritte sono pipelined.

GLI ELEMENTI DI ELABORAZIONE

Nella figura e’ raffigurata la configurazione di ognuno dei PE che costituiscono il vettore di processori in una generica architettura SIMD.

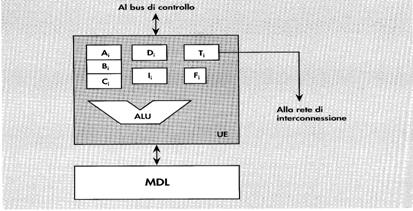
Ogni elemento di elaborazione e’ costituito da una memoria dati locale MDL e da una unita’ di elaborazione che contiene una ALU e un insieme di registri scalari.

L’indice i associato a ogni registro indica che il registro appartiene all’i-esimo PE.

In particolare:

· Ai,Bi,Ci costituiscono un banco di registri di lavoro di uso generale.

· Ii, e’ un registro indice predisposto per contenere un offset tramite il quale indirizzare i singoli dati presenti nella propria MDL.

· Di e’ un registro che consente di indirizzare un qualsiasi altro PE.

· Ti e’ il registro di trasferimento: rappresenta la sorgente o la destinazione per le operazioni di trasferimento dati tra diversi PE.

· Fi e’ il flag che indica lo stato del PE. Solamente i PE abilitati concorrono all’esecuzione dell’istruzione distribuita dalla UC.

Da un punto di vista logico, un problema di fondamentale importanza per l’efficienza dell’elaborazione e’ una efficace distribuzione degli operandi vettore tra le diverse MDL da parte dell’Unita’ di controllo.