Documento word
Documento zippato
Documento PDF
Esercizio
Si vuole scrivere un sottoprogramma che effettui la
moltiplicazione di un numero contenuto nel registro E per 8 e depositi il
risultato nel registro DE.
Analisi
Notiamo anzitutto che, dato un numero binario
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
se effettuiamo una traslazione verso sinistra di una
posizione di ogni bit del dato
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
aggiungendo uno zero al bit meno significativo,
abbiamo effettuato una moltiplicazione per due. Infatti il dato di partenza era
l’equivalente binario del numero 54 mentre il dato risultante dalla traslazione
è l’equivalente binario del numero 108 = 54*2.
È intuitivo che la moltiplicazione per otto si possa
ottenere traslando il dato originario a sinistra per tre volte.
Questa operazione prende il nome di shift a sinistra.
Possiamo dire, con un brutto neologismo, che potremo effettuare la
moltiplicazione per otto del contenuto del registro E, shiftando tale registro
verso sinistra per tre volte.
L’analisi non è completa. Cosa avviene infatti ai bit
più significativi durante le traslazioni? Appare ovvio che questi bit “vengono
espulsi” dal dato ma non possiamo lasciare che vengano persi.
Se abbiamo, ad esempio, il seguente dato (+40)
|
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
e lo shiftiamo verso sinistra otteniamo
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
Se shiftiamo ancora una volta otteniamo
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
Qui si dovrebbe fare notare che il bit più
significativo è diventato 1, quindi il numero andrebbe considerato un numero
negativo, ma di questo ci occuperemo dopo. Quello che ci preme far notare, è
che l’ulteriore shift porterebbe al seguente risultato
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
Con l’espulsione del bit più significativo dal dato si
avrebbe che 40*8=64!
In realtà il problema consiste nel fatto che non ci
siamo preoccupati del fatto che, con probabilità, moltiplicando un dato ad otto
bit per 8 otteniamo un valore che necessita di un numero maggiore di bit per
essere rappresentato.
Il problema si risolve utilizzando due registri ad
otto bit di cui uno conterrà il dato originario e l’altro sarà destinato ad
ospitare i bit via via espulsi dal primo registro. Nel nostro esempio avremo
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
cioè
256+64=320 = 40*8
Resta un ultimo particolare relativo al segno. È
evidente che un numero negativo deve rimanere negativo dopo la moltiplicazione
mentre un numero positivo deve rimanere positivo. Allora, se, ad esempio,
abbiamo il seguente numero
|
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
corrispondete al numero –24 ( se facciamo il
complemento a due otteniamo 00011000 = +24), moltiplicando per otto dovremmo
ottenere
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
cioè –24*8 = - 192 ( infatti, in complemento a due
abbiamo 0000000011000000 = 128+64 = 192).
Per fare ciò basta imporre che, all’inizio, prima di
effettuare gli shift, se il numero di partenza è positivo, il registro di
appoggio dovrà essere posto a zero mentre se il numero di partenza è negativo,
il registro di appoggio dovrà avere tutti i bit ad 1. In tal caso, il segno del
risultato dovrà essere automaticamente rispettato.
Diagramma di flusso
Prima di passare al diagramma di flusso approfittiamo
per dire un’altra cosa relativa al passaggio di parametri fra programma
principale e sottoprogrammi. Il programma principale deve passare al
sottoprogramma il dato da moltiplicare. Per com’è definita la traccia appare
ovvio che lo scambio di questo dato avverrà attraverso il registro E. il
risultato viene passato dal sottoprogramma al programma principale attraverso
il registro DE. È evidente dunque che è levito aspettarsi che il sottoprogramma
modifichi il contenuto di questi due registri e questo è anzi un effetto voluto
altrimenti i due moduli non riuscirebbero a scambiarsi informazioni. Ma ciò
vale per qualsiasi registro? La risposta è no. Immaginate che il programma
principale memorizzi nel registro A un dato importante e che questo registro
venga utilizzato dal sottoprogramma per i suoi calcoli interni, il risultato
sarebbe disastroso, poiché, al rientro dal sottoprogramma, il programma
principale non troverebbe più in A il dato che vi aveva memorizzato. È
necessario, allora, quando parte un sottoprogramma, salvare per prima cosa i
registri che questi andrà a modificare, fatta eccezione per i registri
utilizzati per scambiare i dati con il programma principale.
La flow chart sarà allora la seguente
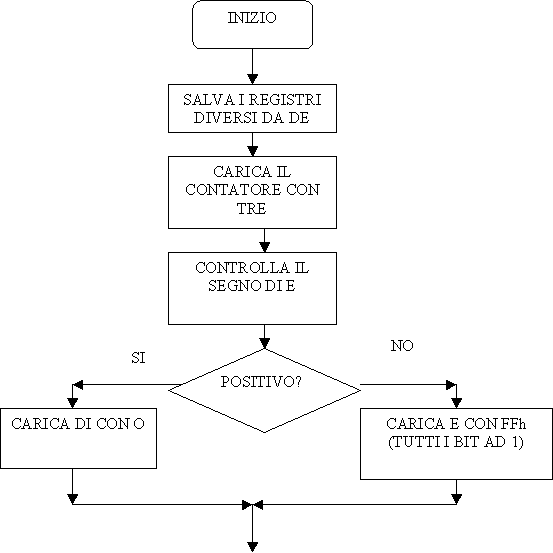
Dobbiamo fare tre shift per cui occorre un contatore di programma. Occorre poi effettuare lo shift a sinistra del dato contenuto in E, prelevare il bit più significativo che viene espulso da E, shiftare a sinistra il dato contenuto in D e accodare ad esso il bit espulso da E
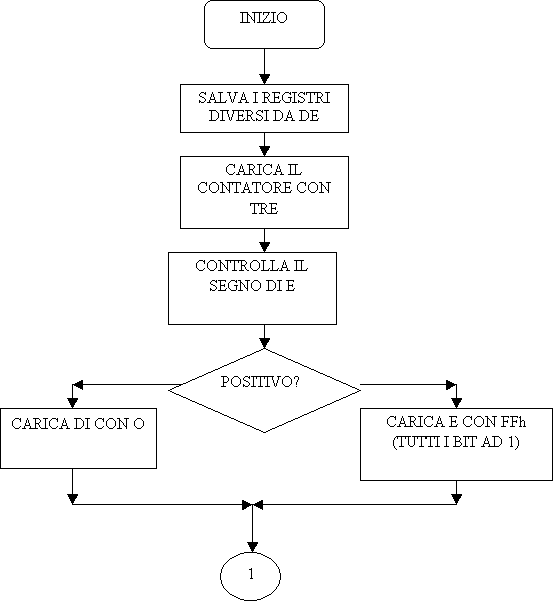
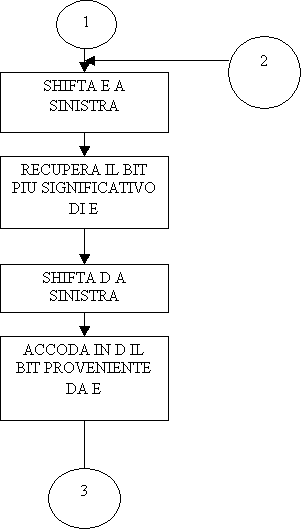
Non resta che decrementare il contatore e controllare se si deve ripetere il ciclo
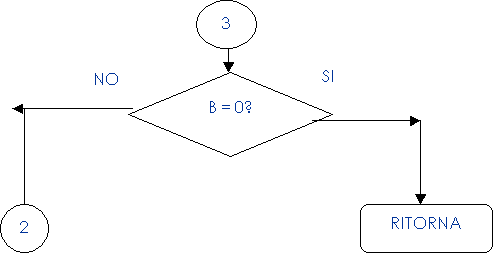
Dobbiamo raffinare il nostro algoritmo. Come facciamo a shiftare a sinistra il registro E? Nel set di istruzioni dello Z80 esiste l’istruzione di shift.
SLA m
Quest’operazione effettua lo shift a sinistra del dato m: ogni bit viene spostato al posto del bit che si trova alla sua sinistra. Al posto del bit zero viene inserito uno zero. Il vecchio contenuto del bit sette viene posto nel flag di carry.
Modifica del registro dei flag
|
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
|
|
|
0 |
|
|
0 |
|
Il flag S funziona come flag di segno, e rappresenta
il segno del dato dopo lo shift
Il flag Z funziona come flag di zero
H viene posto sempre a zero
Il flag PV funziona come flag di parità
Il flag N è posto sempre a zero
Il flag di carry conterrà il bit sette del dato
L’operando m può essere un registro ad otto bit
dello Z80
Es. SLA C
Prima
3C
10
C F
Dopo
0 7 6 5 4 3 2 1 0 0 1 1 1 1 0 0 0
10
C F
78
|
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
0 |
0 |
|
0 |
|
1 |
0 |
0 |
Il risultato dello shift è stato un numero positivo
(S=0)
Il risultato dello shift è stato un numero diverso
da zero (Z=0)
Il risultato dello shift presenta un numero di bit
ad uno pari a quattro (numero pari) per cui PV=1
Il bit sette del dato prima dello shift era zero per
cui C = 0
L’operando m può essere un operando di memoria il
cui indirizzo si trova nel registro HL (indirizzato in modo indiretto)
L’operando m può essere il contenuto di una
locazione di memoria il cui indirizzo si ottiene sommando il contenuto di un
registro indice (IX o IY) ad uno spiazzamento (indirizzamento indicizzato)
Quindi il blocco
SHIFTA E A SINISTRA si può realizzare con un’unica istruzione. Dall’analisi
dell’istruzione sappiamo anche che il bit più significativo espulso dal
registro E viene immagazzinato nel flag di carry del registro dei flag.
Il problema
diventa allora quello di prelevare il flag di carry e accodarlo a D. per fare
questo possiamo utilizzare l’istruzione ADC
ADC
A, s
Quest’istruzione esegue la somma fra il
contenuto dell’accumulatore, il secondo operando s ed il flag di carry
|
ADC A, r |
Indirizzamento a
registro |
Si somma all’accumulatore il contenuto del
registro ad otto bit r (A, B, C, D, E, H, L) |
|
ADC A, n |
Indirizzamento immediato |
Si somma all’accumulatore il contenuto del
dato ad otto bit immediatamente espresso nell’istruzione |
|
ADC A, (HL) |
Indirizzamento indiretto |
Si somma all’accumulatore il contenuto
della locazione di memoria il cui indirizzo è dato dal contenuto del registro
HL |
|
ADC A, (IX+d) |
Indirizzamento indicizzato |
Si somma all’accumulatore il contenuto
della locazione di memoria il cui indirizzo è dato dal contenuto del registro
IX sommato allo spiazzamento d espresso nell’istruzione |
|
ADC A,(IY+d) |
Indirizzamento indicizzato |
Si somma all’accumulatore il contenuto
della locazione di memoria il cui indirizzo è dato dal contenuto del registro
IY sommato allo spiazzamento d espresso nell’istruzione |
Modifiche
al registro dei flag
|
S |
Z |
|
H |
|
P/V |
N |
C |
|
|
|
|
|
|
|
0 |
|
Il
flag S verrà settato a seconda del segno del risultato
Il
flag Z verrà settato se il risultato è nullo
Il
flag H verrà settato se vi sarà un riporto fra il quarto e il quinto bit
Il
flag PV verrà settato se vi sarà un errore di overflow
Il
flag N è a zero trattandosi di una somma
Il
flag c verrà settato se vi è un riporto sull’ottavo bit
Esempio: ADC
A, 1A
Prima
Il
contenuto del registro dei flag è dispari. Ciò vuol dire che il bit meno significativo
(il flag di carry) è pari ad uno.
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
+
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
+
|
|
|
|
|
|
|
|
1 |
=
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
Abbiamo il riporto fra il primo ed il
secondo nibble, per cui H=1, il risultato è positivo per cui S=0, il risultato
è non nullo per cui Z=0, non vi è un riporto sull’ottavo bit per cui C=0, il
risultato rientra nel range –128/+127 per cui PV=0.
Dopo
Appare allora la possibilità di risolvere il
nostro problema. Basta infatti fare la somma fra un accumulatore in cui
preventivamente abbiamo posto il contenuto a zero, il registro D e il flag di
carry.
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
+
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
+
|
|
|
|
|
|
|
|
1 |
=
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Alla fine l’accumulatore contiene il
contenuto di D a cui è stato accodato il flag di carry. Basta dunque spostare
il contenuto di A in D per completare l’opera. Per non fare errori occorre fare
attenzione al fatto che il registro D va shiftato a sinistra prima del registro
E altrimenti nel flag di carry va a finire il bit più significativo di D e non
di E.
La flow chart diventa allora
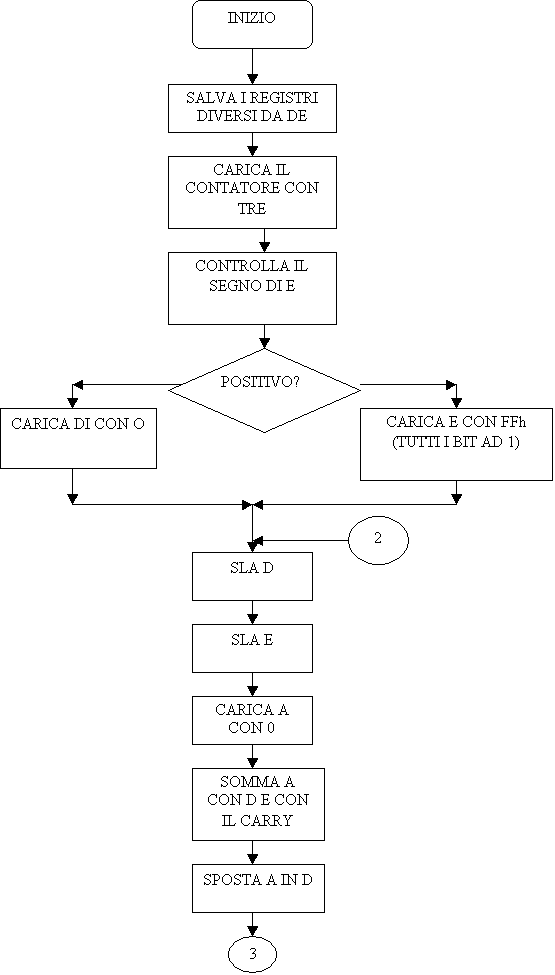
SI
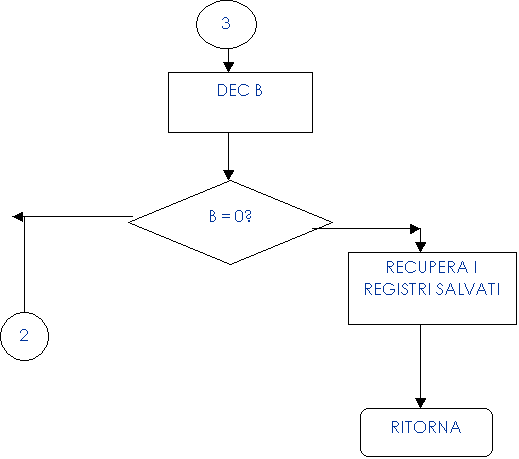
Listato assembly
Per creare un sottoprogramma basta associare
alla sua prima istruzione un’etichetta che costituirà il nome del
sottoprogramma. Inoltre per salvare i registri che verranno modificati (e che
ora sappiamo essere A e B) potremmo pensare di utilizzare i registri gemelli.
Ricordiamo, però, che per salvare B nel banco dei registri gemelli dovremmo
utilizzare l’istruzione EXX
EX
AF, AF’
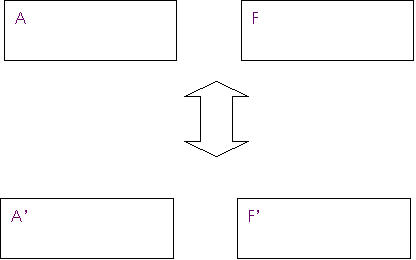
L'istruzione
scambia il contenuto di A ed F con A' ed F'
Esempio
Contenuto dei registri prima dell’esecuzione
dell’istruzione
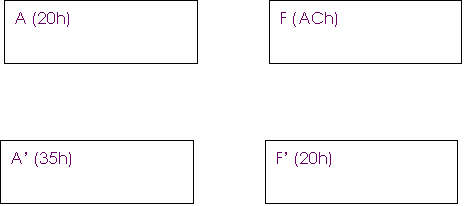
Contenuto dei registri dopo
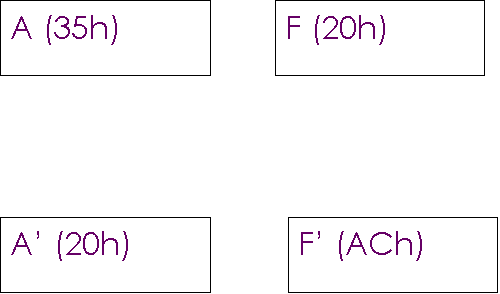
L’istruzione EXX consente invece di scambiare tutti registri BC, DE, HL con BC’, DE’, HL’
Esempio.
Prima
Dopo
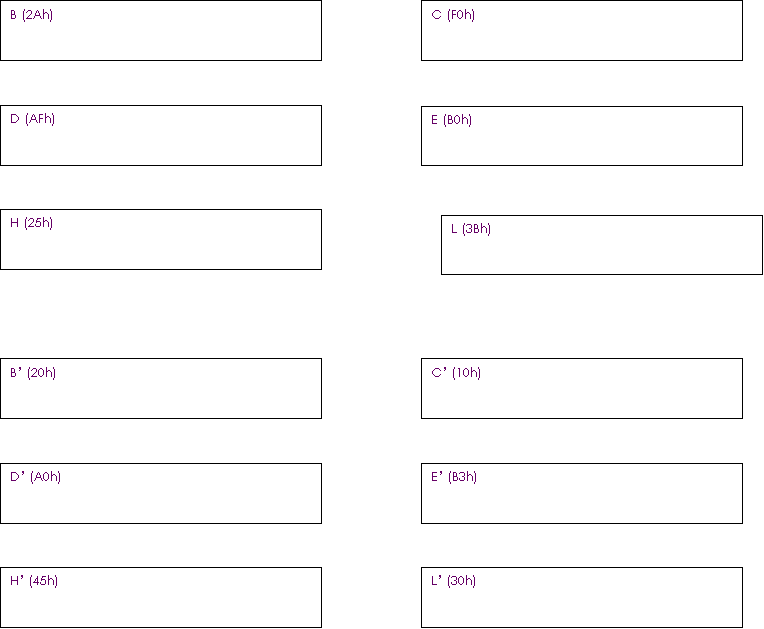
In sostanza, utilizzando l’istruzione EXX, perderemmo il contenuto del registro E, per cui il sottoprogramma girebbe non più sul dato passatogli dal programma principale nel registro E ma sul dato presente nel banco dei registri gemelli.
In alternativa possiamo salvare i registri nello stack con le istruzioni
PUSH
qq
Con
quest’istruzione la coppia di registri o registro a 16 bit qq viene spinta in
cima allo stack. Ricordiamo che lo Stack Pointer punta all’ultima locazione
riempita dello stack e che questo cresce occupando le locazioni di memoria che
hanno indirizzo via via decrescente.
Allora la parte alta del registro qq va nella prima locazione
libera, quindi nella locazione il cui indirizzo si ottiene dall’indirizzo
contenuto in SP meno uno, mentre la parte bassa di qq va nella locazione
successiva, quindi nella locazione il cui indirizzo si ottiene dall’indirizzo
contenuto in SP meno due. Poiché lo stack cresce di due locazioni, lo Stack
Pointer va decrementato di due unità
Non
si ha alcun effetto sul registro dei flag.
Esempio: PUSH
DE
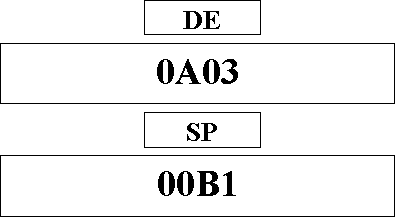Prima
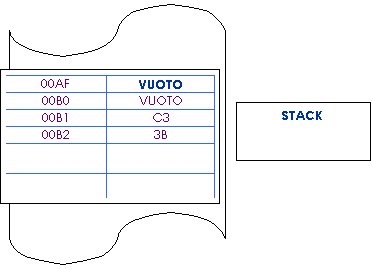
Dopo
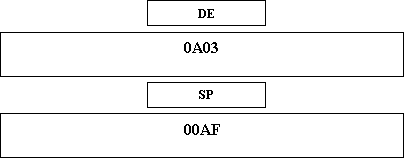
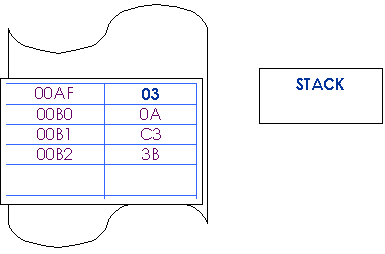
qq
può essere uno dei seguenti registri: BC; DE; HL; AF; IX; IY
Per
recuperare un registro dallo stack occorrerà eseguire l’istruzione
POP
qq
Con
quest’istruzione la coppia di registri o registro a 16 bit qq viene riempita
con il contenuto delle due locazioni di memoria in cima allo. Ricordiamo che lo
Stack Pointer punta all’ultima locazione riempita dello stack e che questo
cresce occupando le locazioni di memoria che hanno indirizzo via via decrescente.
Allora la parte alta del registro qq viene riempita con il
contenuto della penultima locazione occupata, quindi nella locazione il cui
indirizzo si ottiene dall’indirizzo contenuto in SP più uno, mentre la parte
bassa di qq viene riempita con il contenuto della locazione successiva, quindi
nella locazione il cui indirizzo si ottiene dall’indirizzo contenuto in SP.
Poiché lo stack decresce di due locazioni, lo Stack Pointer va incrementato di
due unità
Non
si ha alcun effetto sul registro dei flag.
Esempio: POP
DE
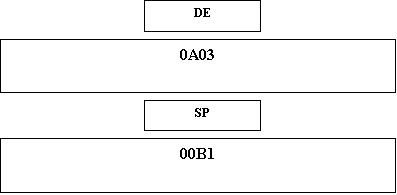Prima
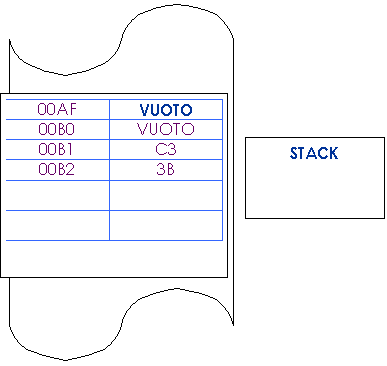
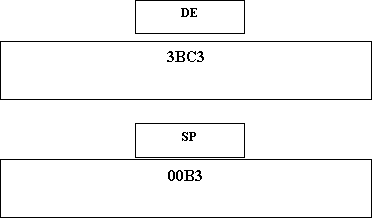Dopo
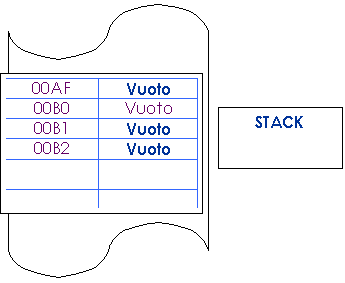
qq
può essere uno dei seguenti registri: BC; DE; HL; AF; IX; IY
In
sostanza possiamo risolvere il nostro problema con una sequenza del genere
Sottoprogramma:
PUSH AF
PUSH BC
Altre istruzioni
POP BC
POP AF
E’
importante notare che, a causa della struttura LIFO dello Stack , occorre
recuperare i dati con l’istruzione di POP in ordine inverso rispetto a quello
con cui sono stati salvati mediante l’istruzione di PUSH.
Non
ci resta che analizzare il modo di eseguire questa parte della flow chart
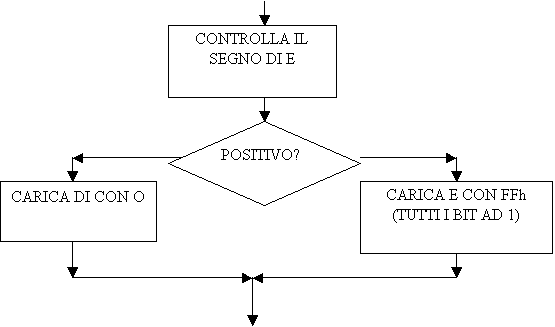
Sappiamo
che per analizzare il segno di un dato basta controllare il suo bit più
significativo per cui la flow chart potrebbe diventare
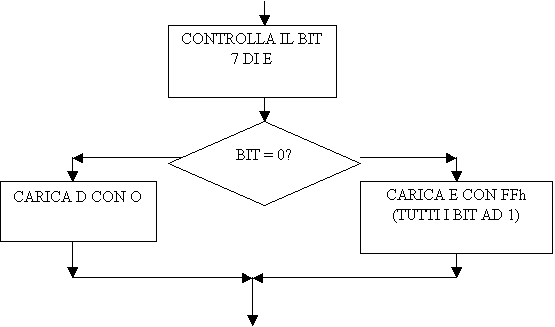
Ma
come possiamo controllare tale bit? Possiamo utilizzare l’istruzione
BIT b, m
Quest’istruzione ha lo scopo di controllare il bit numero b dell’operando m. il risultato del test sarà posto nel flag Z secondo la seguente legge
Se il bit testato risulta pari ad 1,
il flag di zero viene posto pari a 0
Se il bit testato risulta pari a 0, il
flag di zero viene posto pari a 1
Modifica del registro dei flag
|
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
? |
|
|
1 |
|
? |
0 |
|
Il flag S assume un valore casuale
Il flag Z funziona nella modalità
descritta sopra
H viene posto sempre ad uno
Il flag PV assume un valore casuale
Il flag N è posto sempre a zero
Il flag di carry non viene influenzato
dall’operazione e conserva il suo vecchio valore
L’operando m può essere un registro ad
otto bit del microprocessore
Es. Bit 3, D
Prima
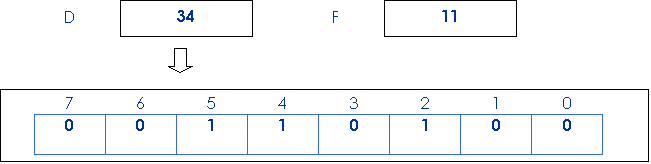
Il bit 3 dell’operando è pari a zero per cui il flag di zero verrà posto ad 1
|
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
? |
1 |
|
1 |
|
? |
0 |
1 |
Il flag di carry è ad 1 poiché tale era il suo valore prima.
L’operando s può essere una locazione
di memoria indirizzata in modo indiretto
Es. Bit 5, (HL)
1C00
10
HL F
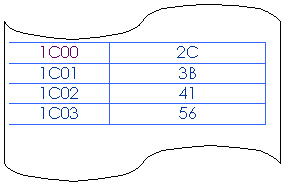
Il bit 5 dell’operando è pari ad uno per cui il flag di zero verrà posto ad 0
|
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
? |
0 |
|
1 |
|
? |
0 |
0 |
L’operando m può essere una locazione
di memoria indirizzata in modo indicizzato
Es, Bit 7, (IX+2)
1C00
10
IX F
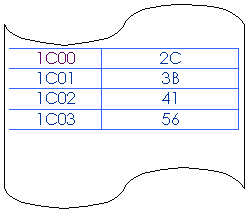
Il bit 7 dell’operando è pari a zero per cui il flag di zero verrà posto ad 1
|
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
? |
0 |
|
1 |
|
? |
0 |
1 |
In sostanza dobbiamo testare il bit 7 del registro E. Se questo bit è a zero dobbiamo eseguire il caricamento di o in D, altrimenti dobbiamo eseguire il caricamento di FF. per realizzare una struttura di questo tipo in assembly dobbiamo giocare nel modo seguente con i salti.
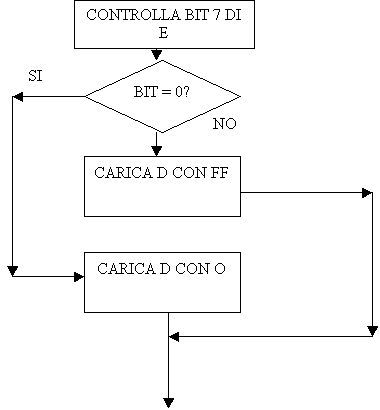
In
sostanza scelgo di testare una condizione , ad esempio controllo se il bit è
uguale a zero (cioè il dato in E è positivo), con un’istruzione di salto
condizionato
Salta
se il bit è uguale a zero
Subito
dopo scrivo l’istruzione da saltare, cioè l’istruzione da eseguire soltanto se
il salto non viene effettuato, cioè se il bit invece di essere a zero si trova
ad 1
Salta
se il bit è uguale a zero alla istruzione che pone D a 0
Metti
in D FFh
Se
questa istruzione viene eseguita, non dobbiamo eseguire l’istruzione che pone D
a zero. Per fare questo dobbiamo effettuare un salto assoluto
Salta
se il bit è uguale a zero alla istruzione che pone D a 0
Metti
in D FFh
Salta
la prossima istruzione
Metti
D a O
Altre
istruzioni
In
assembly dovremmo scrivere una cosa del genere
JP Z, AVANTI
LD D,0FFH
JP CICLO
AVANTI: LD D,00H
CICLO: SLA D
Ricordiamo, infatti, che a causa
dell’istruzione BIT, se E ha un contenuto negativo, il bit 7 di E sarà a zero e
quindi l’esecuzione dell’istruzione di BIOT porterà il flag di zero a 0, quindi
bisogna saltarla se il flag sta ad 1. quindi la condizione da impostare è JP Z,
AVANTI
Il
listato completo del sottoprogramma è
moltiplica: PUSH AF
PUSH BC
LD B,
03H
BIT 7,E
JP Z, AVANTI
LD D,0FFH
JP CICLO
AVANTI: LD D,00H
CICLO: SLA D
SLA E
LD A,00H
ADC A,D
LD
D,A
DEC B
JP NZ,CICLO
POP BC
POP AF
RET
Testiamolo con un programma completo
ORG 0000H
ld e,80h
call moltiplica
halt
moltiplica: PUSH AF
PUSH BC
LD B,
03H
BIT 7,E
JP Z, AVANTI
LD D,0FFH
JP CICLO
AVANTI: LD D,00H
CICLO: SLA D
SLA E
LD A,00H
ADC A,D
LD
D,A
DEC B
JP NZ,CICLO
POP BC
POP AF
RET