Documento word
Documento
Zippato
Documento pdf
Il teorema di Fourier
Nell’analisi dei circuiti basati su operazionali che andremo a studiare, vedremo che cercheremo di ricavare la loro risposta in frequenza. In particolare cercheremo di individuare, dato un ingresso sinusoidale del tipo
S(t) = sen(ωt+α)
quale sarà la forma del segnale sull’uscita del circuito. La natura sinusoidale del segnale garantisce che possiamo usare, nel nostro studio, tutti gli strumenti del metodo simbolico applicati nello studio delle reti interessate da tensioni e correnti sinusoidali isofrequenziali.
Naturalmente si prospetta immediatamente l’esenziale obiezione che, in elettronica, i segnali sinusoidali sono soltanto una minima parte dei segnali di interesse. A cosa serve, allora, la risposta in frequenza, nello studio della risposta di un amplificatore ad un segnale d’ingresso, costituito, ad esempio, da un’onda quadra?
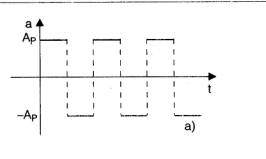
Ci viene in soccorso il teorema di Fourier, secondo il quale, un segnale periodico qualsiasi può essere considerato come la somma d’infinite sinusoidi con caratteristiche diverse. Matematicamente si ha una relazione del tipo
S(t) = A0+A1sen(ωt+φ1)+A2sen(2ωt+φ2)+A3sen(3ωt+φ3)+…
Il termine A0 ( detto anche componente continua) è un termine costante che rappresenta il valor medio del segnale. Se il segnale stesso ha valor medio nullo, come nell’esempio dell’onda quadra di figura, il termine costante A0 non è presente. Si ha poi una sinusoide a frequenza pari a quello del segnale complessivo che viene detta armonica fondamentale. Tutte le altre sinusoidi o armoniche hanno una frequenza multipla di quella fondamentale. La loro ampiezza decresce con l’aumentare della frequenza. Per l’onda quadra di figura, ad esempio, l’ampiezza delle armoniche è pari a
An=0 se n è pari
An=![]() se n è dipari
se n è dipari
Il contenuto armonico di un segnale si può rappresentare graficamente attraverso un diagramma come il seguente
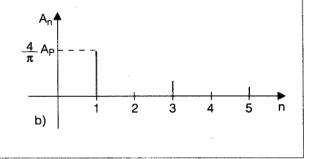
in cui si posiziona una riga in corrispondenza della frequenza di ogni armonica. L’ampiezza della riga rappresenta l’ampiezza dell’armonica. Si noti come nel caso specifico, esistono soltanto le armoniche di ordine dispari.
Nel seguente diagramma notiamo come viene ricostruita l’onda quadra se sommiamo soltanto le prime due armoniche
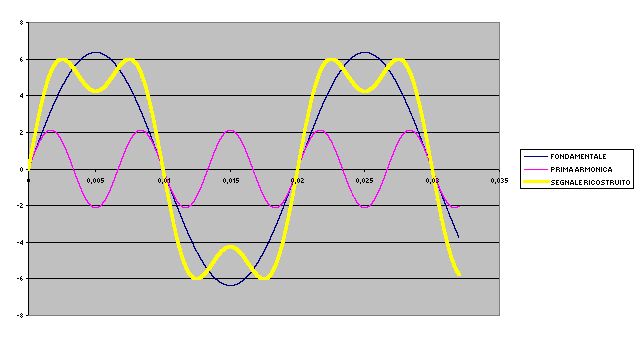
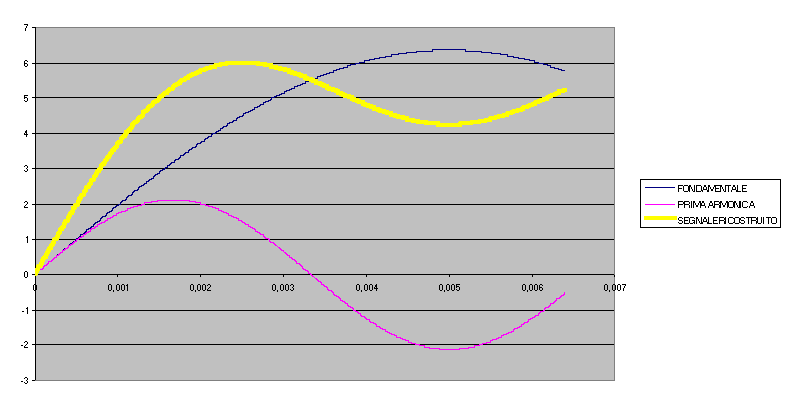
La ricostruzione del segnale è effettuata nei tre docuMENTI ALLEGATI
Potete usare il foglio excel per sperimentare altri parametri del segnale.
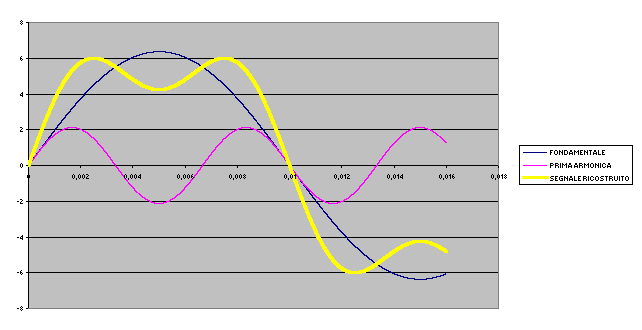
se usiamo invece le prime tre armoniche abbiamo
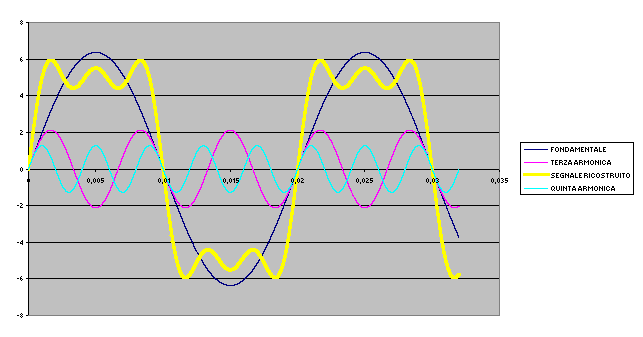
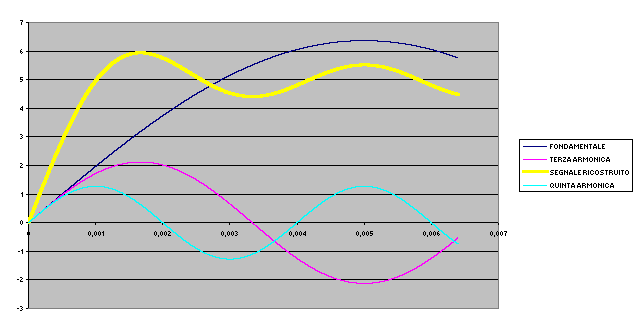
La ricostruzione del segnale è effettuata nei tre docuMENTI ALLEGATI
Potete usare il foglio excel per sperimentare altri parametri del segnale.
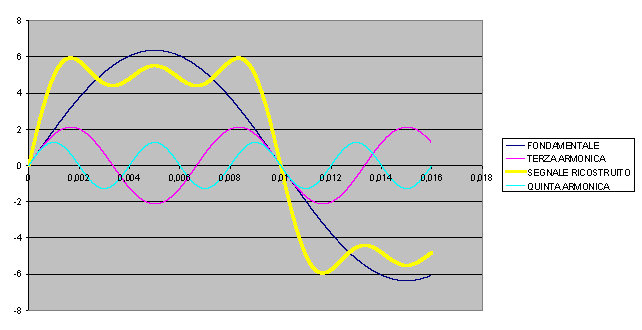
Se usiamo le prime cinque armoniche
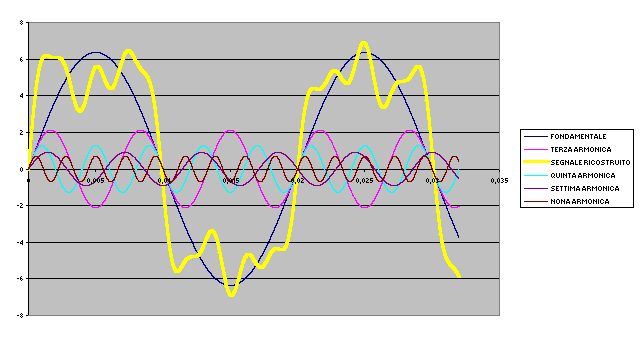
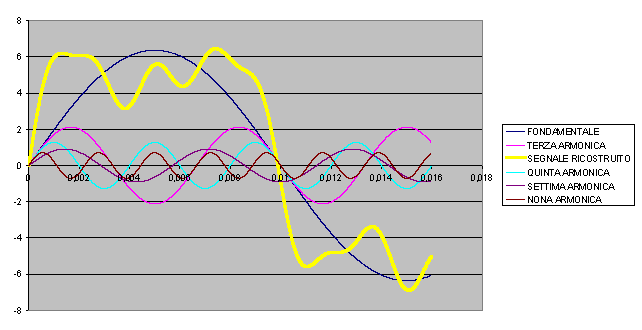
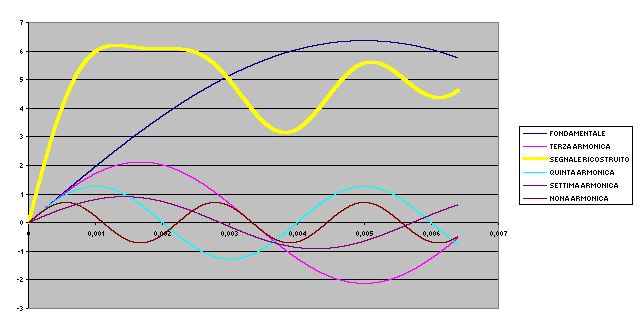
La ricostruzione del segnale è effettuata nei tre docuMENTI ALLEGATI
Potete usare il foglio excel per sperimentare altri parametri del segnale.
notiamo dunque come, mentre teoricamente dovremmo usare un numero infinito di armoniche per ricostruire il nostro segnale, nella pratica bastano le prime n armoniche per ottenere un risultato soddisfacente. Il numero n dipende dal criterio che abbiamo stabilito per definire soddisfacente il risultato.