P R O G E T T O
Sistema Termico per il
calcolo del poterE di inserzione di una ventola
Anno Scolastico 2004-2005
Docenti : prof. ing. Antonio Costantini
prof. ing.
Paolo Rubino
prof. ing.
Antonio Santoro
Candidato : Francesco Dell’Isola
DESCRIZIONE
DEL SISTEMA
Il
seguente sistema, rappresentato nell’immagine sotto riportata, confina la
temperatura di una lastra di materiale termico-conduttivo tra due soglie
attraverso l’utilizzo di un feedback costituito da un sensore termico, da un
comparatore e da una ventola.
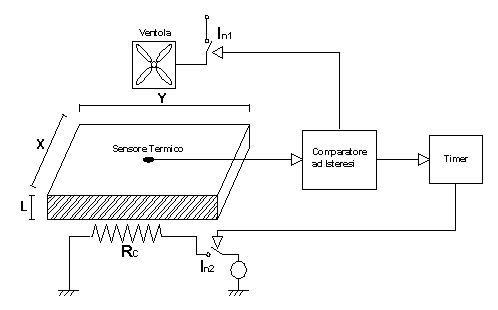
Figura 7 – Schema a Blocchi del Sistema
Essenzialmente
costituito da:
Un Resistore termico avente resistenza elettrica 
;
Una lastra metallica avente
dimensioni X,Y,L;
Alimentatore 
;
Alimentatore 
;
Un sensore termico con scala -40 /
125 °C;
Un comparatore ad isteresi Trigger
di Schmitt;
Una ventola di raffreddamento;
Un timer;
Due interruttori elettronici;
Passiamo ora a descrivere il principio di funzionamento del
sistema:
la
resistenza 
alimentata a mezzo
dell’alimentatore 
per effetto Joule si
riscalda, emettendo calore che viene trasmesso alla lastra metallica con la
quale è posta in contatto; la legge di trasmissione del calore che regola tale
processo è quello del fenomeno di conduzione.
Il
sensore termico che è posto sopra la lastra metallica, rileva la temperatura
raggiunta da questa che viene tramutata in segnale di tensione posto in
ingresso al comparatore ad isteresi. Il segnale che perviene al comparatore ad
isteresi viene confrontato con i valori preimpostati; cioè il valore della
temperatura registrata dal sensore termico viene confrontato con i due valori
di soglia min e max precedentemente inseriti sul comparatore stesso tramite il
dimensionamento delle resistenze che lo costituiscono.
Il sistema
ha quattro stadi di funzionamento:
1. La
temperatura della lastra risulta inferiore ad entrambi i valori di soglia; in
questo caso non si ha alcuna necessità di operare modifiche nel processo in
atto, essendo la piastra ancora in fase di riscaldamento. Quindi il sensore
misura una temperatura minore della temperatura di riferimento inferiore e dà
in uscita una tensione tale che l’uscita del comparatore sia minore di zero.
Questa ultima è posta all’ingresso
dell’interruttore 
che si pone in stato
logico 
andando ad aprire il
circuito di alimentazione della ventola.
2. La
temperatura della piastra risulta compresa tra i valori di soglia; anche in
questo caso non viene operata alcuna modifica del processo in atto, essendo la
temperatura della piastra entro i valori che noi abbiamo impostato come
ottimali.
3. La
temperatura della piastra risulta maggiore al valore di soglia superiore; in
questo caso il sensore in uscita manda una tensione tale che il comparatore da
un’uscita maggiore di zero. Pertanto questa ultima pone l’interruttore 
a livello logico 1
facendolo chiudere. Di conseguenza la ventola viene alimentata aumentando
fortemente lo scambio per convezione che avviene tra la superficie della
piastra e l’aria circostante, dissipando in tal modo parte del calore ceduto
dal resistore alla piastra. Tale fenomeno fa sì che la temperatura della
piastra si abbassi con il trascorrere del tempo con un andamento esponenziale.
4. Allorquando
la temperatura della piastra, rilevata dal sensore termico e trasmessa sotto
forma di segnale di tensione all’ingresso del comparatore ad isteresi, raggiunge
un valore minore del valore di soglia inferiore, in uscita al comparatore si ha
una tensione negativa la quale pone l’interruttore 
allo stato logico 
, facendo aprire il circuito di alimentazione della ventola.
Questa fermandosi, riduce lo scambio di calore per convenzione tra la piastra e
l’aria circostante, consentendo alla piastra di aumentare nuovamente la sua
temperatura.
L’impianto
realizzato, presenta un sistema di sicurezza che è costituito da un timer di
protezione, che si attiva automaticamente allorquando il comando emesso di
azionamento della ventola, non dovesse produrre, per qualsiasi motivo (es.
mancato azionamento dell’interruttore sito sul circuito di alimentazione della
ventola), gli effetti desiderati. Tale timer inizia il conteggio del tempo
trascorso dall’emissione del comando del comparatore, fino a raggiungere il
valore di sicurezza preimpostato. Se entro l’intervallo di tempo preimpostato
la situazione di anomalia del circuito non dovesse cessare, il sistema
interviene sull’interruttore In2 inserito nel circuito di
alimentazione della resistenza elettrica, comandandone l’apertura.
Il sistema innanzi illustrato è stato posto in essere
al fine di salvaguardare le apparecchiature dell’impianto
1. 0. INTRODUZIONE
Lo studio dei fenomeni di trasmissione
del calore riguarda tutti quei processi fisici nei quali una certa quantità di
energia termica è trasferita da un sistema ad un altro a causa di un gradiente
di temperatura.
Tali processi avvengono in accordo con i principi
fondamentali della termodinamica:
1.
il primo principio
della termodinamica afferma che l’energia termica ceduta da un sistema è uguale
a quella ricevuta dall’altro.
2.
il secondo principio
della termodinamica afferma che l’energia termica passa dal sistema a
temperatura più alta a quello a temperatura più bassa.
Nella trasmissione del calore, chiamata
anche Termocinetica, ciò che conta è la rapidità in cui avviene il processo di
scambio termico. Riveste quindi notevole importanza la quantità di calore
scambiata nell’unità di tempo che prende il nome di potenza termica. Essa viene
indicata col simbolo 
e poiché è una
potenza, nel Sistema Internazionale si misura in watt.
1.1 MODALITA’ DI SCAMBIO TERMICO
La trasmissione del calore avviene
spontaneamente solo da un corpo caldo ad uno freddo, fino a che i due corpi
raggiungono la stessa temperatura, detta di equilibrio termico. Il corpo caldo
comunica a quello freddo parte della sua energia termica intensificandone
l’agitazione molecolare.
La propagazione del calore può avvenire
per conduzione, convenzione e o per irraggiamento.
1.2 CONDUZIONE
Il trasferimento per conduzione avviene
tra corpi che sono a contatto, o parti di esso che si trovano a temperature
diverse. Esso è causato dal trasferimento di energia cinetica da una molecola a
quella adiacente che possiede una velocità di vibrazione minore. Poiché la velocità di vibrazione delle particelle è
direttamente proporzionale alla temperatura, il corpo caldo cede energia a
quello freddo, aumentandone la temperatura, finché non è raggiunto l’equilibrio
termico (vedere Figura 1).
Figura 1 - Schema del
Principio della Conduzione Termica
I processi di scambio termico tramite
conduzione sono generalmente classificati in:
Processi
stazionari
Processi
non stazionari o transitori
I primi hanno la caratteristica che tutte
le grandezze fisiche (temperatura, pressione, etc.) in ogni punto della regione
dove si ha conduzione risultano indipendenti dal tempo, mentre i processi
transitori implicano variazioni temporali che il più delle volte interessano la
temperatura.
La legge che descrive i processi
stazionari, non è valida per quelli transitori; per questi ultimi, come vedremo
in seguito, useremo delle relazioni opportune.
1.3 CONVEZIONE
La convezione è un fenomeno che interessa
tipicamente i fluidi e si basa sul trasporto macroscopico di materia. Se
analizziamo lo scambio termico tra un solido ed un fluido, ci accorgiamo che
esiste uno scambio di tipo conduttivo; in Figura 2 è rappresentato il caso di un fluido che interagisce
con una parete solida a temperatura 
.
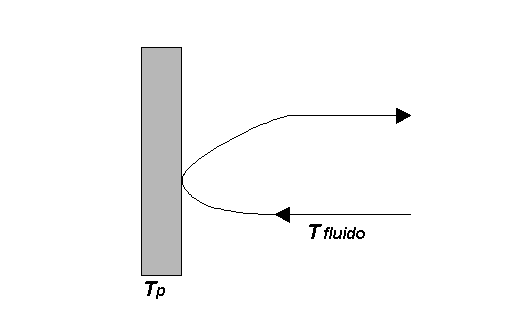
Figura 2 - Schema del
Principio della Convezione
Inizialmente la parete cede calore per
conduzione alle particelle di fluido prossime alla superficie; l’energia così
trasmessa và ad aumentare quella interna del fluido ed è portata via dal
movimento del fluido stesso. In questo caso il moto del fluido è dovuto alla
differenza di densità che si instaura tra diversi strati dello stesso.
La convezione ha luogo quando uno dei due
corpi interessati dallo scambio termico è un fluido, e la trasmissione del
calore può essere associata ad un trasferimento di materia.
In un fluido a temperatura non uniforme,
per effetto combinato di un campo di temperatura e di velocità, si determina
una distribuzione dei valori di densità variabile da punto a punto, conseguenza
dei fenomeni di dilatazione termica. In questi casi le forze gravitazionali
provocano continui movimenti delle particelle del fluido, con conseguente miscelazione,
favorendo pertanto la trasmissione del calore dalle particelle più calde a
quelle più fredde; questo fenomeno prende il nome di convezione naturale.
La trasmissione di calore per convezione
naturale è alla base del funzionamento dei termosifoni, dove, l’aria fredda
passando attraverso le lamelle si scalda e va verso l’alto.
Quando invece i movimenti delle
particelle del fluido sono imposti essenzialmente da cause meccaniche (una
pompa, nel caso di circolazione dell’acqua, o semplicemente l’azione del
vento), il fenomeno prende il nome di convezione forzata, ne è un esempio il
raffreddamento di un radiatore di un’automobile con aria soffiatavi sopra da
una ventola.
Molto spesso i due fenomeni si
intrecciano dando luogo alla convezione mista: è il caso del ventilconvettore dove una ventola
spinge l’aria fredda attraverso le lamelle di un corpo scaldante. Lo scambio
termico convettivo è strettamente legato al moto del fluido ed affonda le sue
radici nella trattazione termodinamica.
1.4 IRRAGGIAMENTO
A differenza delle altre due modalità di
scambio termico, l’irraggiamento non richiede alcun mezzo perché vi sia
trasmissione di energia. La radiazione elettromagnetica è generata in tutte le
direzioni, quindi in questo caso il corpo avente temperatura maggiore emette
radiazioni elettromagnetiche che vengono assorbite dal corpo più freddo (vedere
Figura 3).
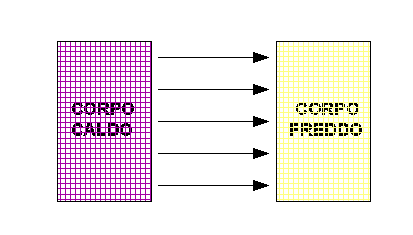
Figura 3 - Schema del
Principio di Irraggiamento
1.5 EQUIVALENTE TERMICO DELLA LEGGE DI OHM
Le considerazioni sulle analogie tra i
fenomeni di scambio di calore, circuito termico equivalente e circuiti elettrici, e in particolare l’ esatta
corrispondenza tra potenza termica e corrente elettrica, sono del tutto
confermate dalla formulazione di una legge fisica chiamata equivalente termico della Legge di Ohm. Essa afferma che la quantità di calore scambiata nell’
unità di tempo, ossia la potenza termica, è direttamente proporzionale alla
differenza di temperatura che causa lo scambio di calore. In simboli:
dove 
è la differenza di
temperatura presente misurata in Kelvin, 
è la potenza termica;
mentre con il simbolo 
si è indicata la
resistenza termica, la cui definizione segue direttamente dalla formula
precedente:
La resistenza termica si misura in 
.
Per fissare la idee sull’analogia tra
fenomeni di scambio di calore e circuiti elettrici, nella Tabella 1 sono state accostate le loro grandezze fisiche e le
due leggi che le legano.
|
Processi
di scambio di calore |
Elementi
elettrici |
|
Equivalente
termico legge di Ohm
|
Legge di Ohm
|
|
Potenza termica |
Corrente |
|
Differenza di temperatura |
Caduta di tensione |
|
Resistenza termica |
Resistenza elettrica |
Tabella 1 - Analogie tra elementi elettrici e processi di scambio
di calore
1.6 LEGGE DI FOURIER
Si definisce densità di flusso termico q
la potenza termica per unità di superficie. Le due dimensioni, nel Sistema
Internazionale, sono quelle di una quantità di calore per unità di superficie.
In simboli:
possiamo enunciare la legge di
Fourier:
è il vettore
rappresentativo della potenza termica;
rappresenta la
superficie isotermica;
è un operatore
vettoriale che trasforma una funzione delle coordinate di un punto in un
vettore le cui componenti cartesiane sono le derivate parziali della funzione
in quel punto.
rappresenta il campo
scalare delle temperature all’ interno di un volume 
di un corpo dove
avviene conduzione.
La proporzionalità tra densità di flusso
termico e gradiente di temperatura, è espressa dal termine 
che prende il nome di
conducibilità termica, che non è grandezza vettoriale ed è caratteristica del
materiale che trasmette il calore e dipende dalla sua natura e dal suo stato
fisico.
ALGORITMO MATEMATICO DEL SISTEMA TERMICO
Calcolo dell’andamento temporale della temperatura
misurata dal sensore:
RT = Ra
// RM
Ciò che noi vogliamo conoscere alla fine del calcolo
dell’algoritmo sotto riportato è:
Possiamo constatare che
la differenza tra i valori equivalenti in tensione delle temperature della
lastra ed ambiente corrisponde ad una somma tra altre due tensioni:
Rispettivamente Va vale:
Si ricava dal passaggio precedente
che:
Sostituiamo a Va il
suo equivalente:
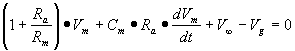
Per semplificare i calcoli poniamo
a0,a1 e a2 con i seguenti valori:
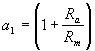
Siamo di fronte ad un’equazione
differenziale del secondo ordine e precisamente nel caso in cui si determinano
due soluzioni reali e distinte:
Ci
calcoliamo ora queste due soluzioni:
Se le
andiamo a sostituire si ottiene:
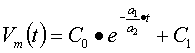
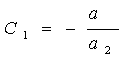
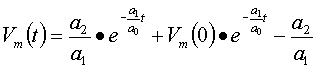
Nel caso in cui volessimo conoscere le tensioni agli istanti
0 si eseguono questi passaggi:
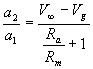
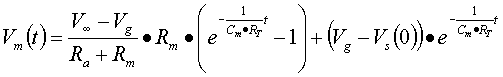
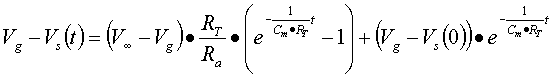
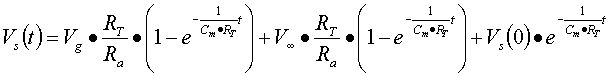
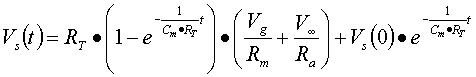
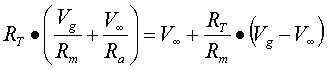
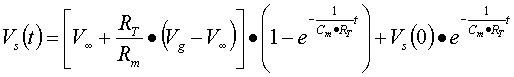
COMPARATORI CON AMPLIFICATORE OPERAZIONALE
3.0 FUNZIONE DEI COMPARATORI
I comparatori sono convertitori che hanno
il compito di confrontare un segnale di tensione ad un riferimento (fisso o
variabile), fornendo all’uscita un segnale in tensione avente due valori.
In particolare, si ha uscita a valore
alto se il segnale supera il riferimento e basso se non lo supera, oppure con
logica invertita.
Poiché in genere il componente
fondamentale dei comparatori è un amplificatore operazionale, per «uscita alta»
si intende la saturazione positiva dell’ amplificatore e per «uscita bassa», la
saturazione negativa.
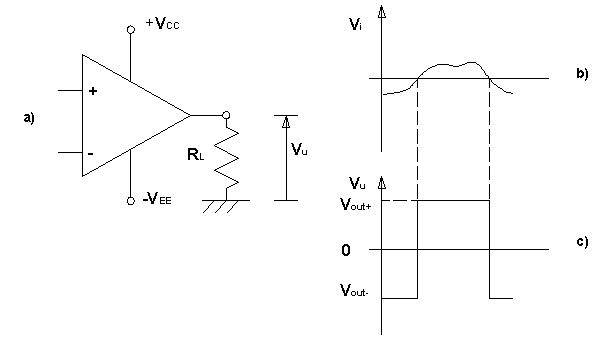
Dalle figure sottostanti si evidenzia che:
In
Figura
4 a) è riportato
il simbolo di un generico comparatore, con il riferimento sull’ingresso invertente
ed il segnale da confrontare sul non invertente; in particolare, nello schema
di figura, il riferimento è al potenziale 
.
In
Figura
4 b) è riportato
l’andamento del segnale d’ingresso, avente valore variabile (positivi e o
negativi)nel tempo.
In
Figura
4 c) è riportato
la corrispettiva uscita del comparatore. Come si osserva, l’uscita si mantiene
al valore di saturazione negativa del comparatore, sino a che l’ingresso è
inferiore al riferimento (nel caso specifico a 0); si porta invece alla
saturazione positiva, allorché l’ ingresso supera il riferimento (cioè lo 0).
Figura 4 - Comparatore,
Andamento del Segnale di Ingresso e della Relativa Uscita
3.1 IMPIEGO DEI COMPARATORI
Grazie al comparatore, è possibile
eliminare gli effetti di indeterminazione causati da valori di segnale prossimi
al riferimento, in quanto il comparatore medesimo dà luogo ad una uscita che
commuta istantaneamente tra due livelli di tensione notevolmente diversi tra
loro, allorché il segnale raggiunge il riferimento.
3.2 COMPARATORI AD AMPLIFICATORI
OPERAZIONALI
L’ amplificatore operazionale in catena aperta
realizza direttamente il comparatore nel rispetto delle definizioni fornite
sopra.
Se infatti ci si pone nell’ipotesi che il
circuito di Figura 3.a) sia un generico amplificatore operazionale, si osserva
che, ponendo l’ingresso invertente a massa ed applicando un segnale al non
invertente, è sufficiente una 
tra i due ingressi:
per portarlo alla saturazione:
Positiva,
se 
;
Negativa,
se
.
Si osservi che 
indica il valore
assoluto della tensione di saturazione d’ uscita; può risultare:
in saturazione posistiva
in saturazione
negativa
Per comprendere l’ordine di grandezza
delle tensioni in gioco, si consideri un amplificatore operazionale con
alimentazioni 
, 
, ed 
.
Risulta:
3.3 IL COMPARATORE DI ZERO NON INVERTENTE
Il comparatore sviluppato nella
precedente esemplificazione, può essere considerato «comparatore di zero», in
quanto rivela, la commutazione dell’ uscita, il passaggio della tensione d’
ingresso attraverso lo zero (vedere Figura 5). Si noti che nella soluzione analizzata, esiste una
zona di insensibilità e per realizzare un comparatore di zero privo di zona di insensibilità, è necessario
ricorrere ad integrati appositi.
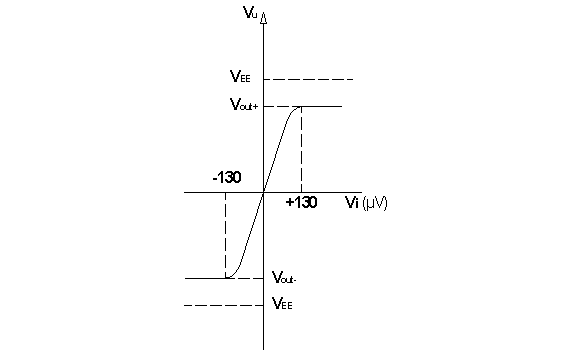
Figura 5 – Caratteristiche
di Trasferimento del Comparatore di Zero non Invertente
3.4 COMPARATORE CON RIFERIMENTO
DIVERSO DA ZERO
Se si considera un sistema di
comparazione che dia luogo a commutazioni dell’ uscita in corrispondenza del
passaggio del segnale d’ ingresso attraverso un valore diverso da zero
(comparatore di livello) si può, come accennato, applicare un potenziale di
tale valore, all’ ingresso non invertente.
La relazione che fornisce il legame tra
l’ uscita e l’ ingresso del comparatore, assume in tal caso l’ espressione:
È tuttavia possibile ottenere comparatori
di livello variabile (da valori positivi a valori negativi), se al diodo zener
si sostituisce un potenziometro, secondo quanto indicato nella sottostante Figura 6 .a).
Nella Figura 6 .b) è riportata la caratteristica di trasferimento di
un comparatore di livello, nel caso in cui il riferimento sia stato fissato ad
un livello positivo 
.
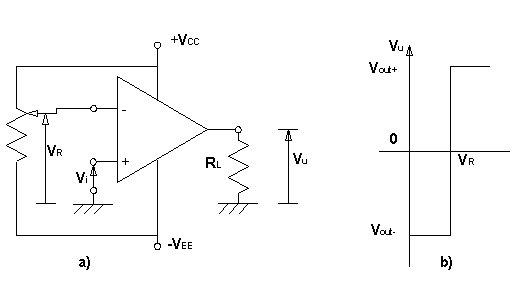
Figura 6 - Comparatore
con Riferimento Diverso da Zero e Caratteristica di Trasferimento
3.5 IL FORMATORE D’ONDA QUADRA
Tra i possibili impieghi del comparatore
di zero, vi è quello che permette di trasformare un segnale sinusoidale in un
onda quadra. In effetti, è possibile applicare all’ ingresso del comparatore di
zero un segnale sinusoidale, per ottenere la commutazione da un livello di
saturazione a quello opposto, in corrispondenza di ciascun passaggio per lo
zero della sinusoide d’ ingresso.
Tali limitazioni sono dovute allo
slew-rate dell’ amplificatore operazionale, che impone di limitare la frequenza
della sinusoide d’ ingresso, se si vuole ottenere all’ uscita un’ onda quadra.
In effetti, se la frequenza della
sinusoide diviene abbastanza elevata, costringe l’ amplificatore operazionale
ad una successione di commutazioni dalla saturazione positiva alla negativa e
viceversa; è possibile che tali commutazioni non giungano a complemento, a
causa dei rallentamenti dovuti allo slew-rate dell’ amplificatore operazionale.
Come è noto, lo slew-rate definisce la
velocità di commutazione dell’ amplificatore operazionale tra i due livelli di
saturazione; in formule:
3.6 COMPARATORE INVERTENTE
Tutte le considerazioni sviluppate
relativamente al comparatore con segnale applicato all’ ingresso non
invertente, restano valide se si applica il riferimento all’ ingresso non
invertente ed il segnale all’ invertente.
La differenza sostanziale dei due
sistemi, consiste nel segno della tensione di saturazione d’ uscita che, in
questo caso, è negativa se il segnale d’ ingresso supera il riferimento e
positiva se ne rimane inferiore (vedere Figura 7).
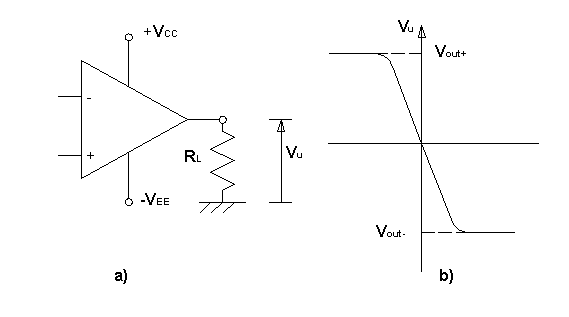
Figura 7 - Comparatore
Invertente con Funzione di Trasferimento
3.7 COMPARATORI AD AMPLIFICATORI OPERAZIONALI CON ISTERESI
I comparatori esaminati precedentemente
presentano una zona di insensibilità, che se per certi versi può rappresentare
uno svantaggio, per altri è utile e conviene addirittura aumentarne l’
ampiezza.
Se ad esempio, al segnale in esame si
sovrappone un rumore, l’ elevata sensibilità del comparatore può dar luogo a
ripetute commutazioni all’ uscita; tali commutazioni non risultano provocate
dal segnale, ma dal rumore ad esso sovrapposto.
È evidente che, aumentando la zona di
insensibilità, si evitano le commutazioni indesiderate causate dal rumore.
Un ulteriore vantaggio ottenibile dall’
aumento della zona di insensibilità, è rappresentato dalla possibilità di
diversificare i livelli di tensione d’ ingresso per i quali si ha commutazione.
Questo significa che, potendo modificare
la zona di insensibilità, si riesce a far si che il comparatore commuti per un
livello di riferimento se il segnale è in fase crescente e per un livello
diverso, se è in fase decrescente.
La zona di insensibilità prende il nome
di isteresi ad
è possibile variarne l’ entità mediante l’ applicazione di un circuito che
realizza una reazione positiva sull’ amplificatore operazionale.
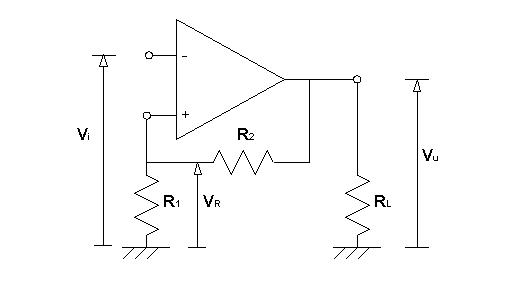
Figura 8 – Comparatore con Isteresi
Dall’analisi della figura si trae che l’
isteresi è ottenuta portando all’ ingresso di riferimento di un normale
comparatore invertente, il segnale presente all’ uscita, mediante un partitore
resistivo formato dalle resistenze 
ed 
.
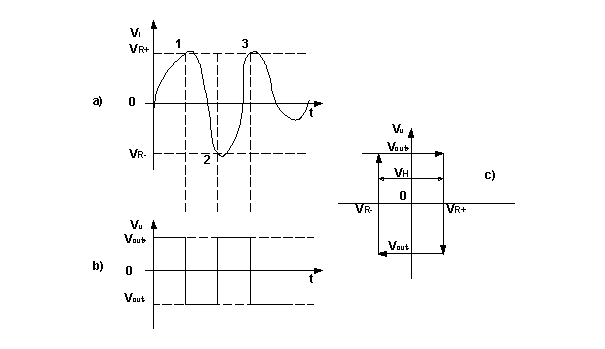
Figura 9 - Ciclo di
Isteresi
Per comprendere l’ effetto della
disposizione circuitale in esame, ci si ponga nella condizione iniziale
riportata all’ istante t = 0 in Figura 9 a).
Come si osserva, nell’ istante iniziale
la tensione all’ ingresso invertente è minore di quella al non invertente; il
comparatore è in saturazione positiva e, all’ ingresso non invertente, viene
mantenuto un potenziale:
Con la modifica del
livello di saturazione d’ uscita da 
a 
, si ha la simultanea
modifica del livello di tensione portato all’ ingresso di riferimento, che
diviene:
In effetti, all’ ingresso di riferimento è ora
presente una tensione 
eguale in modulo a 
, ma di segno opposto.
Per avere una commutazione dalla
saturazione negativa alla positiva, è necessario che la tensione 
si porti al di sotto
del livello di riferimento 
.
La differenza tra i due livelli di
riferimento rappresenta l’ isteresi ottenuta per mezzo della reazione positiva
sul comparatore.
La tensione di isteresi vale dunque:
Infine:
3.8 TRIGGER DI SCHMITT
Il circuito analizzato in precedenza,
offre la possibilità di modificare le soglie di tensione in corrispondenza
delle quali avviene la commutazione dell’uscita, ma tali soglie risultano
comunque simmetriche rispetto al potenziale zero.
E’ possibile ovviare a questa
limitazione, realizzando un comparatore con isteresi, nel quale le soglie di
commutazione non sono più necessariamente simmetriche rispetto allo zero.
Tale comparatore viene comunemente detto trigger di Schmitt e vede il
comparatore di zero sino ad ora esaminato, come caso particolare.
Per ottenere un trigger di Schmitt, è
sufficiente inserire, nella rete di reazione positiva del comparatore di zero,
una tensione di riferimento 
.
Tale tensione nella Figura 10 a) sotto riportata è stata ottenuta, per semplicità,
mediante un generatore di tensione di valore 
; nella pratica, si ricorre invece ad un partitore che
fornisce 
a partire dalla
tensione di alimentazione 
o 
(vedere Figura 10 b).
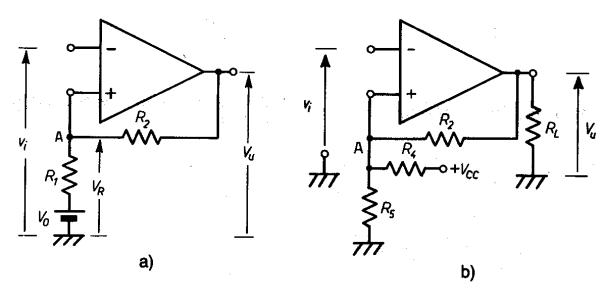
Figura 10 - a) Trigger con tensione di
riferimento V0 (Batteria) ; b) Trigger con tensione di riferimento V0
ottenuta da + Vcc
E’ possibile dimostrare che , con gli
schemi sopra raffigurati si ottengono, per le soglie le relazioni che seguono,
ove si è indicata genericamente con 
la tensione d’
uscita, che diviene 
in saturazione
positiva e 
in saturazione
negativa.
ove si è posto:
La tensione di isteresi conserva invece
il valore espresso mediante la formula precedente, ovvero:
4.0 INTRODUZIONE
Il
Simulatore Termico è un tool sviluppato in ambiente LabView .
Il
seguente tool è uno strumento virtuale per comprendere in modo più approfondito
la dinamica del sistema termico in analisi.
Il
Simulatore Termico è composto dalle
seguenti finestre di interfaccia:
Lastra
Sorgente
Ventola
Sensore Termico
Comparatore
Simulatore Termico
Le connessioni
delle suddette finestre sono riportate in Figura 11 :
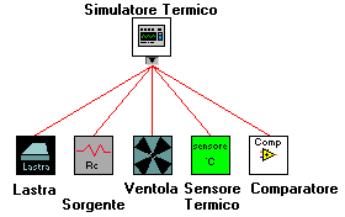
Il
Tool si presenta inizialmente attraverso la finestra “Simulatore Termico” per
mezzo la quale si accede alle ulteriori interfacce che costituiscono il
simulatore con la seguente logica di successione riportata in Figura 12:
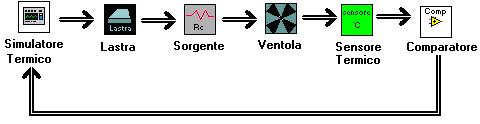
Nei
successivi paragrafi del seguente capitolo verrà approfondito il funzionamento
di ogni finestra di interfaccia.
4.1 FINESTRA DI
INTERFACCIA “LASTRA”
La finestra di interfaccia
denominata “Lastra” visualizzata nella figura sottostante (
Figura 13) è uno
strumento virtuale che permette all’utente di identificare le dimensioni e il
tipo di materiale della lastra in modo da calcolare automaticamente le
caratteristiche termodinamiche di quest’ultima.
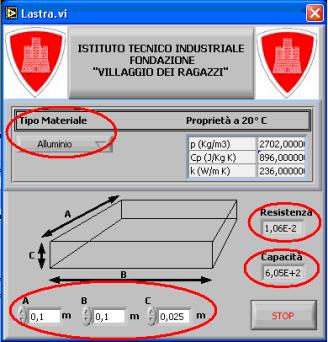
Figura 13 - FINESTRA DI
INTERFACCIA “LASTRA”
La
scelta del tipo di materiale che costituisce la lastra e di conseguenza le
costanti caratteristiche termodinamiche viene eseguita attraverso la selezione
di un elemento del menù a tendina “Tipo Materiale” .
Selezionato
il materiale e le dimensioni della
lastra vengono calcolate automaticamente le seguenti grandezze fisiche:
Resistenza termica
Capacità termica
Si osserva che i valori calcati sono
relativi ad una lastra che ha come spessore “C” un valore di un ordine di
grandezza inferiore rispetto al valore della larghezza “B” e della lunghezza
“A” della lastra.
4.2 FINESTRA DI INTERFACCIA “SORGENTE”
La
finestra di interfaccia “Sorgente” ” visualizzata nella figura sottostante (Figura 14) permette di
inserire il valore della Temperatura ambiente e della Temperatura superficiale
del resistore che ha la funzione di sorgente termica.
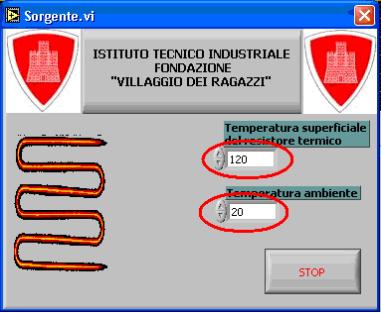
Figura 14 - FINESTRA DI
INTERFACCIA “SORGENTE”
Si osserva
che il Tool simulatore termico pone la temperatura iniziale del sistema termico
pari alla temperatura ambiente.
4.3 FINESTRA DI
INTERFACCIA “VENTOLA”
La
finestra di interfaccia “Ventola”, visualizzata nella figura sottostante (Figura 15), permette attraverso l’immissione dei valori
“Conduttanza Superficiale Unitaria” (relativa alla lastra quando la ventola è
disalimentata) e “Coefficiente Moltiplicativo” (relativo all’effetto convettivo
presente sulla superficie della lastra quando la ventola è alimenta) di
calcolare e visualizzare i seguenti valori:
Resistenza Superficiale della
lastra a ventola alimentata
Resistenza Superficiale della
lastra a ventola disalimentata
Temperatura superficiale della
lastra a regime quando la ventola è disalimentata
Temperatura superficiale della
lastra a regime quando la ventola è alimentata
Figura 15 - FINESTRA DI
INTERFACCIA “VENTOLA”
4.4 FINESTRA DI
INTERFACCIA “SENSORE TERMICO”
Nella
finestra di interfaccia “Sensore Termico” ”, visualizzata nella figura
sottostante (Figura
16), viene
diagrammata la funzione di trasferimento del sensore di temperatura LM60.
Inoltre vengono calcolati i valori di tensione limite di uscita del
sensore attraverso l’immissione dei
valori limite di Temperatura della lastra.
Questi
ultimi, per un corretto funzionamento di tutto il sistema, devono rispettare la
seguente condizione:
Essi
devono sempre essere all’interno del range delimitato dai valori di Temperatura
a regime precedentemente calcolati nella finestra “Ventola”.
I
valori di tensione limite del sensore di temperatura oltre a essere
visualizzati numericamente vengono diagrammati sul grafico in modo da essere
rapportati con la FDT del sensore di temperatura.
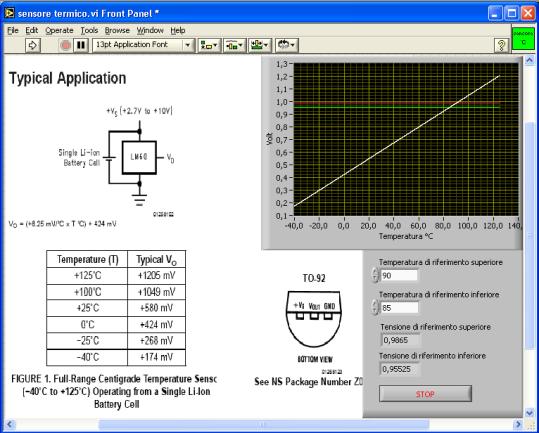
Figura 16 - FINESTRA DI
INTRFACCIA “SENSORE TERMICO”
4.5 FINESTRA DI
INTERFACCIA “COMPARATORE”
Nella
finestra di interfaccia “Comparatore”, visualizzata in Figura
17, viene dimensionato il comparatore trigger di
schmitt. Si osserva che il dimensionamento del comparatore (valore della
resistenza R2) viene eseguito ponendo come default i seguenti valori:
Tensione di alimentazione
dell’amplificatore operazionale = ±12 Volts
Tensione della batteria di
riferimento = 5 Volts
Resistenza R1=10 kΩ
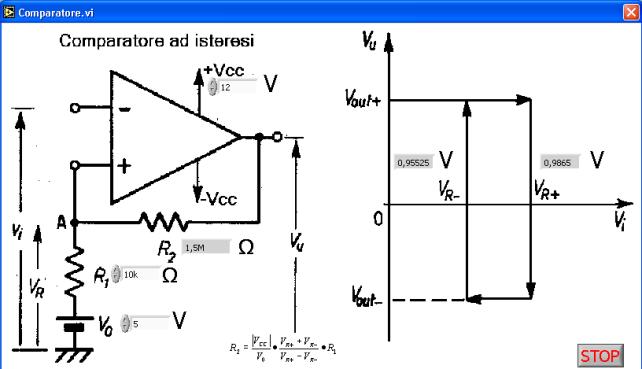
Figura 17 - FINESTRA DI
INTERFACCIA “COMPARATORE”
4.6 FINESTRA DI INTERFACCIA “SIMULATORE TERMICO”
Eseguita
la corretta identificazione del sistema termico attraverso l’immissione delle
variabili nelle finestre di interfaccia precedentemente illustrate, il tool
mostra la finestra “Simulatore Termico”, visualizzata in Figura 18. In questa vengono rappresentati su un grafico l’andamento
della temperatura del sensore (grafico di color bianco) e l’andamento temporale
dell’alimentazione della ventola (grafico di color rosso).
Inoltre
nella finestra è presente una rappresentazione animata del sistema termico
composto dagli elementi principali elencati in introduzione. L’animazione è
sincronizzata con la dinamica del sistema stesso.
Ulteriori
dati calcolati e visualizzati sono:
Il numero di volte che la ventola
viene alimentata nell’unita di tempo minuto.
Il tempo ,espresso in millisecondi,
in cui la ventola viene alimentata in un singolo periodo.
Il
Simulatore termico simula anche un dispositivo di sicurezza per eventuali
guasti, attraverso un interruttore che disalimenta la ventola e un timer che
apre l’interruttore “Power Rc”.
Il timer
inizia il conto dopo che la temperatura del sensore supera la temperatura di
riferimento superiore e apre l’interruttore quando il conteggio supera il
valore di 5 secondi.
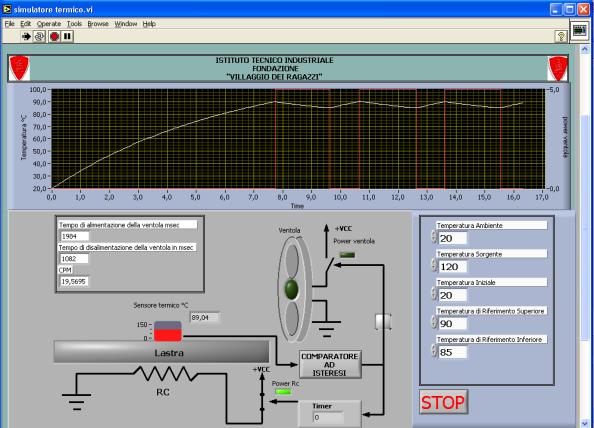
Figura 18 - FINESTRA DI
INTRFACCIA “SIMULATORE TERMICO”
a) DATA SHEETS LM 60.pdf
b) DATA SHEETS
BIBLIOGRAFIA
“Fondamenti di Trasmissione del Calore” – Vol I
R.
Mastrullo – P Mazzei – V. Naso – R. Vanoli
Ed.LIGUORI – UNA
Indice
DESCRIZIONE DEL SISTEMA 1
TRASMISSIONE DEL CALORE 4
1. 0. INTRODUZIONE 4
1.1 MODALITA’ DI SCAMBIO TERMICO 4
1.2 CONDUZIONE 5
1.3 CONVEZIONE 6
1.4 IRRAGGIAMENTO 7
1.5 EQUIVALENTE TERMICO DELLA LEGGE DI OHM 8
1.6 LEGGE DI FOURIER 9
ALGORITMO MATEMATICO DEL SISTEMA
TERMICO 10
COMPARATORI CON AMPLIFICATORE
OPERAZIONALE 14
3.0 FUNZIONE DEI COMPARATORI 14
3.1 IMPIEGO DEI COMPARATORI 15
3.2 COMPARATORI AD AMPLIFICATORI
OPERAZIONALI 15
3.3 IL COMPARATORE DI ZERO NON INVERTENTE 16
3.4 COMPARATORE CON RIFERIMENTO
DIVERSO DA ZERO 17
3.5 IL FORMATORE D’ONDA QUADRA 18
3.6 COMPARATORE INVERTENTE 19
3.7 COMPARATORI AD AMPLIFICATORI OPERAZIONALI CON ISTERESI 20
3.8 TRIGGER DI SCHMITT 22
SIMULATORE SISTEMA TERMICO 25
4.0 INTRODUZIONE 25
4.1 FINESTRA DI INTERFACCIA
“LASTRA” 26
4.2 FINESTRA DI INTERFACCIA
“SORGENTE” 27
4.3 FINESTRA DI INTERFACCIA
“VENTOLA” 28
4.4 FINESTRA DI INTERFACCIA
“SENSORE TERMICO” 29
4.5 FINESTRA DI INTERFACCIA
“COMPARATORE” 30
4.6 FINESTRA DI INTERFACCIA
“SIMULATORE TERMICO” 30
APPENDICE 32
BIBLIOGRAFIA 32