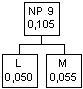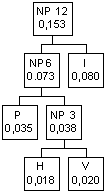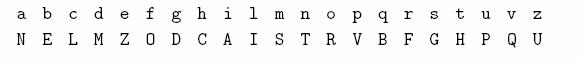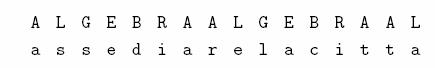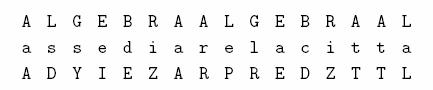Il Livello di presentazione

La codifica dei dati

Scopo fondamentale del livello di presentazione è quello di permettere di dialogare a computer che usano codifiche diverse per rappresentare i dati.

Se un computer dovesse inviare dati ad un altro computer che usa codifiche diverse, il trasmettitore dovrebbe trasformare i dati codificandoli nel formato utilizzato dal computer ricevitore prima di spedirli. Questa soluzione prevede che un computer, per dialogare con tutti i computer presenti nella rete, deve conoscere tutti i loro sistemi i codifica.

Si potrebbe pensare alla soluzione in cui è il computer ricevente ad occuparsi della transcodifica dei dati ricevuti nel formato che egli utilizza. In questo caso è il computer ricevente a dover conoscere tutti i tipi di codifica utilizzati nella rete cui esso è collegato.

La soluzione ottimale è che, a livello di sessione sia stabilita una sorta di codifica universale o codifica di riferimento e che ogni computer ricevente deve trasformare i suoi dati secondo questa codifica prima di inviarli, ed il computer ricevente li debba trasformare dal codice di riferimento nel proprio codice. Con questa soluzione tutti i computer devono conoscere soltanto il proprio sistema di codifica e quello di riferimento.

La compressione dei dati.

Il livello di sessione si occupa anche del problema di comprimere i dati in modo da ridurre i tempi di trasmissione.

Un primo caso è quello in cui i dati appartengano ad un insieme di valori finiti, che hanno tutti la stessa probabilità di essere trasmessi.

Un esempio potrebbe essere quello di una filiale di una ditta commerciale che deve trasmettere ogni giorno alla sede centrale il codice dell’articolo venduto in ogni transazione. Supponiamo che siano venduti 100000 articoli al giorno e che il codice id ogni articolo sia formato da 13 byte (dimensione del codice a barre). In questo caso dovranno essere trasmessi 100.000*13=1.300.000 byte per fornire informazioni sui prodotti venduti ogni giorno. Supponiamo ora che il numero di articoli possibili nel catalogo della ditta sia di 10.000. La soluzione più semplice, in luogo di trasmettere il codice a barre del prodotto, è quella di identificare ogni articolo con un numero intero. Per rappresentare 10.000 articoli occorrono dunque gli interi da 0 a 9999, ma per rappresentare 10.000 combinazioni diverse bastano 2 byte = 16 bit è 2¹⁶ = 65.536 combinazioni possibili diverse. In tal caso, sostituendo al codice a barre un numero intero, per la trasmissione dei dati relativi alla vendita di 100.000 articoli basteranno 100.000*2 = 200.000 byte.

Un caso diverso è quello della trasmissione di simboli non equiprobabili, cioè di simboli la cui probabilità non è identica, come nel caos di un testo scritto in cui le varie lettere dell’alfabeto non hanno la stessa probabilità. In tal caso si usano tecniche in cui il codice usato per rappresentare il simbolo è tanto più corto quanto maggiore è la probabilità che il simbolo debba essere trasmesso.

Tecnica di Huffmann

Un esempio è la tecnica di Huffman. Per prima cosa occorre possedere una tabella in cui sia indicata la probabilità di ogni simbolo

Simbolo	Probabilità
A	0,129
B	0,040
C	0,047
D	0,029
E	0,088
F	0,023
G	0,032
H	0,018
I	0,080
L	0,050
M	0,055
N	0,056
O	0,100
P	0,035
Q	0,008
R	0,060
S	0,070
T	0,044
U	0,012
V	0,020
Z	0,004
Probabilità totale	1

Mettiamo i simboli in ordine crescente di probabilità

Simbolo	Probabilità
Z	0,004
Q	0,008
U	0,012
H	0,018
V	0,020
F	0,023
D	0,029
G	0,032
P	0,035
B	0,040
T	0,044
C	0,047
L	0,050
M	0,055
N	0,056
R	0,060
S	0,070
I	0,080
E	0,088
O	0,100
A	0,129
Probabilità totale	1

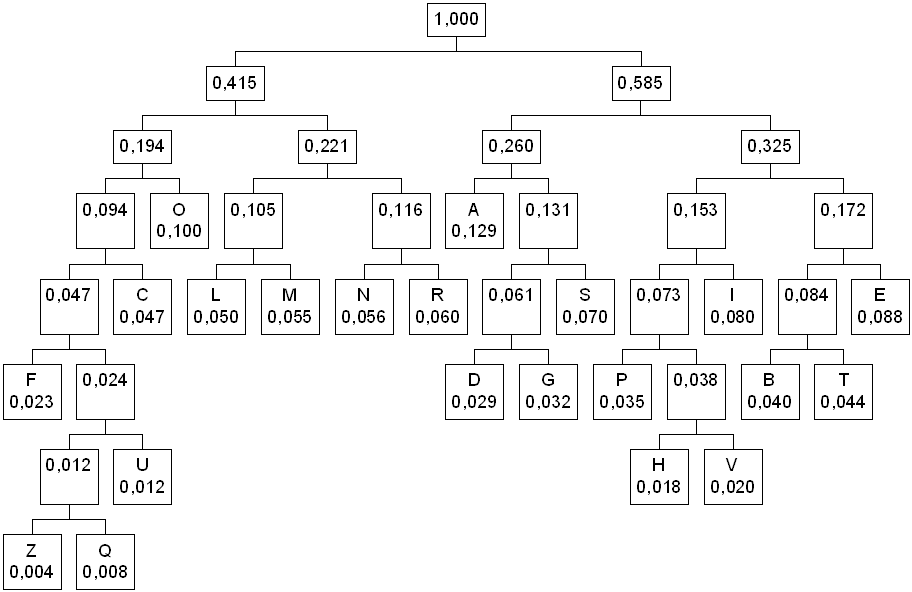
A questo punto si costruisce un albero delle probabilità secondo il seguente algoritmo: si scorrono i simboli a partire da quelli a probabilità inferiore; se trovo due simboli che hanno una probabilità inferiore a nodi già presenti nell’albero, costruisco un nuovo nodo a cui unisco i due nodi suddetti come foglie ed associo al nuovo nodo una probabilità data dalla somma delle probabilità dei due simboli. Se trovo un solo simbolo a probabilità inferiore ad uno dei nodi già presenti nell’albero, unisco il simbolo e tale nodo come foglie di un nuovo nodo che avrà ancora come probabilità la somma delle probabilità delle due foglie.

Esemplifichiamo con le probabilità della tabella di esempio.

Si scelgono i due simboli che secondo la tabella hanno probabilità minore, in questo caso Z e Q

I due nodi vengono uniti ad un nodo padre la cui probabilità è la somma delle probabilità dei nodi figli cioè 0,004+0,008 = 0,012

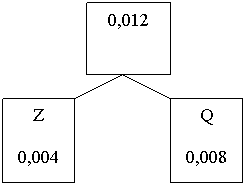
Ora, guardando la tabella si nota che tutti i simboli hanno una probabilità superiore a quella di questo nodo padre tranne il simbolo U che ha la stessa probabilità, allora U diventa un nodo dell’albero e viene unito insieme a tale nodo ad un nuovo nodo padre

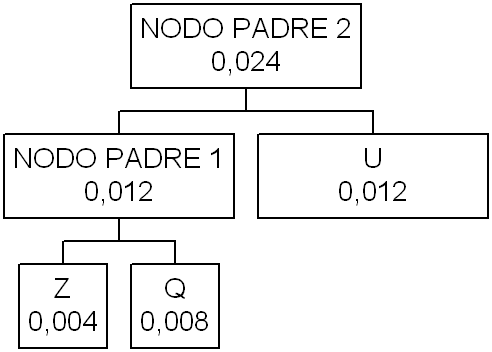
Il nuovo nodo padre è caratterizzato da una probabilità complessiva di 0,024. scorrendo la tabella si nota che i caratteri H e V hanno entrambi probabilità inferiore a quella del nodo padre appena inserito per cui vanno collegati ad un nuovo nodo padre differente dal precedente

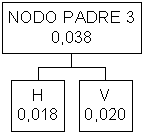
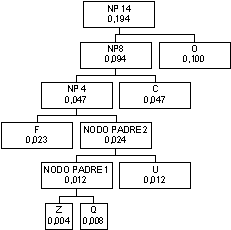
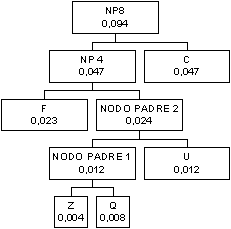
Se ora guardiamo alla tabella abbiamo che il carattere F ha probabilità 0,023, poi viene il nodo padre 2 con probabilità 0,024, poi il nodo D con probabilità maggiore a quella del nodo padre 2, per cui vanno uniti F ed il nodo padre 2 ad un nuovo nodo padre

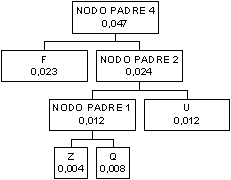
I nodi D e G hanno probabilità inferiore a quella di tutti i caratteri rimanenti e dei nodi padri introdotti per cui vanno collegati ad un nuovo nodo padre

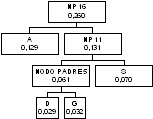
Fra i caratteri rimanenti quello con probabilità inferiore ora è P(0,035) poi viene il nodo padre 3 (0,038). Essi vanno perciò uniti in un nuovo nodo padre

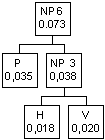
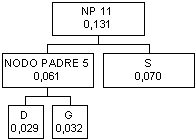
I nodi B (0,040) e T (0,044) hanno probabilità inferiore a quella dei nodi padri 4, 5 e 6 per cui vanno collegati ad un nuovo nodo padre

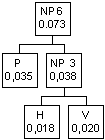
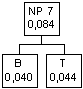
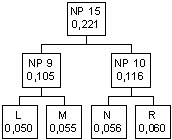
IL carattere C ha probabilità 0,47, il carattere L viene subito dopo con probabilità 0,050, che è superiore a quella del nodo padre 4 (0.047) per cui vanno collegati C e il nodo padre 4 ad un nuovo nodo padre

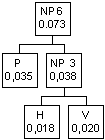
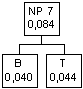
L (0,050) e M (0,055) hanno probabilità inferiore a quella di tutti i nodi padri, per cui vanno collegati ad un nuovo nodo padre indipendente

per formare il codice corrispondente ad un simbolo si procede partendo dal nodo padre dell’albero e prendendo nota delle diramazioni che occorre prendere per raggiungere il carattere prescelto. Se si deve procedere verso sinistra si aggiunge un bit 0 al codice, se si va a destra si aggiunge un bit 1. Ad esempio, per giungere al nodo A si deve andare

Ø A destra ->1

Ø A sinistra ->10

Ø Ancora a sinistra -> 100

Il codice per A sarà 100

Per V invece

Ø A destra ->1

Ø A destra ->11

Ø A sinistra ->110

Ø A sinistra ->1100

Ø A destra ->11001

Ø A destra ->110011

Si noti che più bassa è la probabilità del simbolo, più in basso esso si troverà sul grafico e più lungo sarà il suo codice.

In alcune applicazioni alcuni caratteri compaiono con una frequenza molto superiore a quella degli altri. Ad esempio, nel caso della trasmissione di immagini formato bitmap, vi sono lunghe sequenze di bit pari ad 1. in tali casi si usa una tecnica detta di codifica per sequenza completa di simbolo ripetuto in cui le lunghe sequenze di bit uguali vengono sostituite dalla trasmissione del numero di caratteri uguali presenti nelle sequenze. Ad esempio, nella trasmissione delle immagini bitmap, poiché i bit 0 sono molto più frequenti degli 1, si trasmette solo una sequenza di valori numerici ciascuno dei quali indica il numero di 0 che sono compresi fra due bit ad 1.

Esempio: la sequenza

0000010000000011000000000000001

diventa

5 8 0 14

perché vi sono 5 zeri prima del primo bit ad 1, poi 8 zeri fra il primo ed il secondo 1, non vi sono bit a zero fra il secondo ed il terzo bit ad 1, ed infine vi sono 14 zeri fra terzo e quarto bit ad 1. Supponendo che occorrano 4 bit per rappresentare ciascuno di questi numeri (perché sappiamo ad esempio che i simboli non si possono ripetere per più di 15 volte) invece di trasmettere tutti i 31 bit originari dovremo trasmettere soltanto 4X4=16 bit.

Crittografia

IL livello di presentazione si occupa anche di tecniche per mantenere la riservatezza delle informazioni mediante tecniche di crittografia.

Il primo esempio storico di tecnica crittografica è il codice di Cesare che consiste semplicemente nel sostituire ad ogni carattere quello che lo segue nell’alfabeto di un numero prefissato di posizioni.

Nell’esempio seguente la frase viene crittografata sostituendo ad ogni carattere quello che lo segue dopo tre posizioni nell’alfabeto

Decrittare un codice del genere è estremamente semplice poiché basta fare 26 tentativi per ricostruire il messaggio. Un miglioramento si può ottenere se il carattere che deve sostituire quello presente nel messaggio originario viene scelto in modo casuale (cifrario monoalfabetico). Non `e facile tuttavia ricordarsi dell’alfabeto cifrante, ossia della trasformazione necessaria per decodificare il messaggio: ci si dovrebbe ricordare di tutta la sequenza delle lettere che saranno senza un particolare schema che ne faciliti la memorizzazione, ovvero bisogna ricordare la permutazione, cosa che non `e in generale più semplice. C’è però un buon sistema per produrre una permutazione dell’alfabeto che si presti ad essere memorizzata facilmente: ed è quello di usare una chiave che sia determinata essa stessa da una parola chiave o da una frase chiave, comunque da una stringa di lettere che possiamo ricordare facilmente.

Facciamo un esempio che chiarisca il procedimento. Supponiamo di avere scelto ome frase chiave la seguente:

Nel mezzo del cammin di nostra vita.

Si procede così: si eliminano tutti gli spazi fra le lettere della frase chiave e si eliminano le lettere ripetute. Nel nostro caso si ottiene:

nelmzodcaistrv.

L’alfabeto cifrante sarà costruito disponendo nell’ordine, sotto l’alfabeto in chiaro, prima le lettere della parola chiave modificata come sopra, e poi le lettere dell’alfabeto in chiaro che non compaiono nella frase chiave, secondo il normale ordine alfabetico. Si avrà allora:

Se il messaggio che vogliamo trasmettere è

dopo la codifica diventa

Un ulteriore progresso sono i codici polialfabetici che consistono nell’utilizzare, per crittografare il testo, più codici monoalfabetici. Un esempio è il cifrario di Vigenère. In questo cifrario si utilizzano i codici di Cesare ed esiste una parola chiave che indica, per ogni lettera del testo da crittografare, quale codice monoalfabetico va usato. Se, ad esempio, la parola chiave è PRECIPITOSO, la prima lettera del testo da crittografare va sostituita utilizzando un codice di Cesare in cui alla lettera A corrisponde la lettera P, la seconda lettera del testo va sostituita utilizzando un codice in cui alla lettera A corrisponde la lettera R, e così via.

Facciamo ancora una volta un esempio. Supponiamo che la parola chiave sia ALGEBRA e di volere crittografare la frase

Assediare la città

Si forma una tabella in cui l aprima riga è la parola chiave ripetuta tante volte senza spazi bianchi in modo da raggiungere la stessa lunghezza della frase da cifrare senza spazi bianchi

Prendiamo ora la tabella di Vigenere e consideriamo le righe che iniziano con le lettere A, L, G, B, R, A della parola chiave. La prima lettera del messaggio (la lettera a) dovrà essere codificata mediante la riga del codice che inizia con A. La seconda lettera dovrà essere codificata mediante la riga del codice che inizia con L, la terza con la riga che inizia con G e così via.

Il risultato finale sarà il seguente

Altro metodo può essere il cifrario di trasposizione in cui si cambia l’ordine dei caratteri che appaiono nel testo da crittografare. Vediamo il seguente esempio

Il testo crittografato è stato ottenuto leggendo il testo originario per colonne, leggendo prima le righe dispari e poi le righe pari