 Documento
word
Documento
word
 Documento
zippato
Documento
zippato
 Documento
PDF
Documento
PDF
Stati indistinguibili e minimizzazione di un automa
Cerchiamo di comprendere anzitutto il concetto di indistinguibilità. Un automa è un sistema (di natura meccanica, elettrica o qualsivoglia) che presenta uno o più ingressi ed una o più uscite

Supponiamo di non conoscere la struttura del sistema. Possiamo analizzarne il comportamento in maniera sperimentale, inserendo in ingresso una sequenza di valori di prova e analizzando la sequenza di valori di uscita.
Consideriamo ad esempio l’automa caratterizzato dalle seguenti tabelle di transizione di stato e trasformazione di uscita
|
VI |
a |
b |
|
VI |
a |
b |
|
1 |
3 |
2 |
|
1 |
0 |
0 |
|
2 |
2 |
3 |
|
2 |
1 |
1 |
|
3 |
3 |
5 |
|
3 |
0 |
0 |
|
4 |
5 |
6 |
|
4 |
0 |
0 |
|
5 |
2 |
1 |
|
5 |
1 |
1 |
|
6 |
1 |
2 |
|
6 |
0 |
0 |
A tali tabelle corrisponde il seguente diagramma degli stati
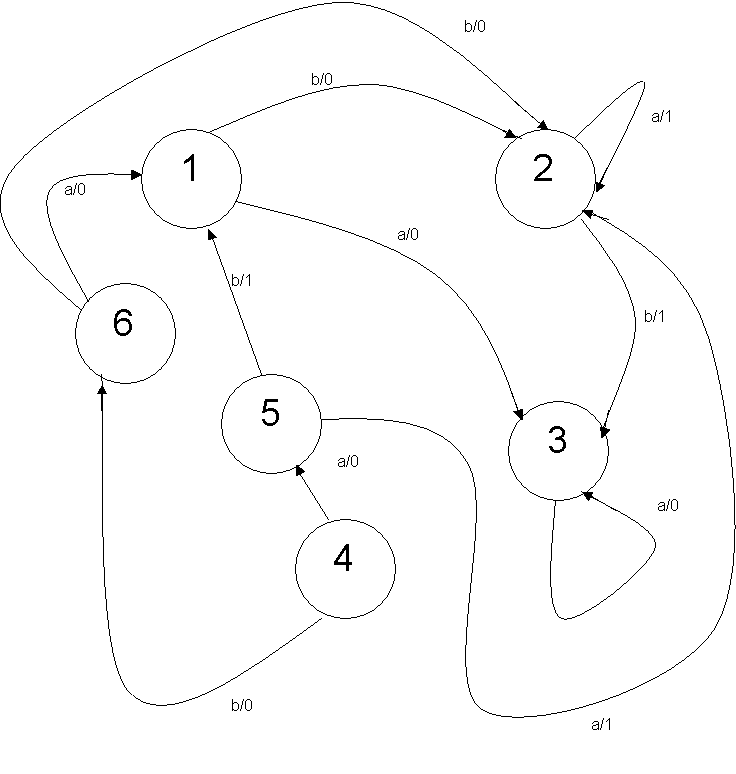
Supponiamo di non avere queste informazioni sull’automa e applichiamo una sequenza di ingresso, per osservare la seguente sequenza di uscita (vedi foglio excel di simulazione)
|
sequenza |
stato |
sequenza |
|
b |
3 |
1 |
|
b |
5 |
0 |
|
b |
1 |
1 |
|
b |
2 |
0 |
|
a |
2 |
1 |
|
b |
3 |
1 |
|
a |
3 |
0 |
Naturalmente la sequenza di valori che osserviamo in uscita dipenderà dallo stato iniziale del nostro automa come si può vedere dai seguenti esempi
Ora osserviamo le sequenze che si ottengono applicando la stessa sequenza di ingresso a partire dagli stati 2 e 5. osserviamo che otteniamo le stesse sequenze di uscita
Nei seguenti esempi
vediamo che, applicando la medesima sequenza di ingresso, otteniamo la stessa sequenza di valori in uscita, sia che partiamo dallo stato 2 sia che partiamo dallo stato 5. Possiamo allora affermare che non possiamo distinguere questi due stati analizzando il comportamento in uscita del sistema. Negli esempi che abbiamo fatto abbiamo applicato sequenze di ingresso composte da più di 200.000 valori, ma, come potete verificare personalmente, lo stesso risultato si ottiene sia che applichiate un miliardo di ingressi, sia che applichiate mille miliardi di ingressi, sia che applichiate una sequenza di infiniti ingressi. Dopo che avete finito di verificare le uscite con un numero infinito di ingressi vi rendete conto che i due stati 2 e 5 risultano indistinguibili . La cosa è per noi importante, perché, se riflettiamo, ci accorgiamo che se due stati danno sempre lo stesso risultato in uscita, noi possiamo semplificare il nostro automa sostituendo questi due stati con un unico stato. In effetti questo automa semplificato darebbe, in corrispondenza della medesima sequenza di ingresso, lo stesso risultato in uscita. Fatelo per esercizio, eliminate lo stato 5 ad esempio, e applicate una sequenza infinita di valori in ingresso al sistema originario e a quello semplificato e osserverete la stessa sequenza di uscita. Un otto a chi fa l’esercizio.
Diamo ora delle definizioni: due stati diversi i e J
potrebbero essere indistinguibili se effettuiamo osservazioni con sequenze di
ingresso lunghe k valori, ma potremmo osservare valori diversi in uscita se applichiamo
un nuovo ingresso k+1. Allora i due stati i e j non sono indistinguibili ma si
dicono semplicemente indistinguibili in k passi. Si dice anche che
formano una classe di k-equivalenza o che sono k-equivalenti.
Ritornando al problema della minimizzazione, osserviamo che
sarebbe molto utile poter conoscere quali sono gli stati indistinguibili in odo
da ottenere automi dalla struttura più semplice. Sembra però, che la
definizione di indistinguibilità non sia di utilità pratica. Se torniamo al
nostro automa di esempio, per controllare se gli stati 2 e 5 sono
indistinguibili in due passi dovremmo applicare tutte le possibili sequenze di
ingresso di due valori (visto che abbiamo solo due valori possibili, a e b,
sono 22 sequenze). Per verificare se sono indistinguibili in 10
passi dovremmo applicare e verificare 210 0 1024 sequenze diverse.
Per verificare se sono indistinguibili in un miliardo di passi dovremmo
applicare 21.000.000.000 sequenze diverse e non saremmo sicuri se in
corrispondenza del valore di ingresso i ordine un miliardo + 1, l’automa non
comici a diversificare il proprio comportamento in uscita. Occorre un metodo di
minimizzazione diverso, non basato sulla definizione. Questo metodo si ottiene
ribaltando la nostra ottica. Invece di verificare se due stati sono
indistinguibili, controlliamo quali sono distinguibili.
Cominciamo con il verificare quali ingressi sono distinguibili. Per prima cosa costruiamo la cosiddetta tabella di equivalenza. E’ una tabella che ha tante righe e tante colonne quanti sono gli stati dell’automa. In questa tabella ogni cella corrisponde ad una coppia di stati. Ora contrassegniamo con una x ogni cella corrispondente ad una coppia di stati distinguibili al primo passo. Gli stati distinguibili al primo passo sono quegli stati che danno, fin dal primo valore di ingresso, valori diversi in uscita. Notiamo , ad esempio, che gli stati 1 e 2 danno valori diversi in uscita, sia che applichiamo l’ingresso a sia che applichiamo l’ingresso b. Allora contrassegniamo la cella 1-2 e la cella 2-1 (corrispondono alla stessa coppia 1-2) con una x
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
|
X |
|
|
|
|
|
2 |
X |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
Procedendo notiamo che gli stati 1 e 3 danno gli stessi valori in uscita, con un ingresso, quindi non possiamo distinguerli in un solo passo (forse sono distinguibili e forse non, per il momento non lo sappiamo) allora le celle corrispondenti nella tabella di equivalenza rimangono vuote. Lo stesso discorso vale per la coppia di stati 1-4. se andiamo alla coppia 1-5, notiamo che avremo valori diversi in uscita, per cui segniamo le caselle 1-5 e 5-1
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
|
X |
|
|
X |
|
|
2 |
X |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
X |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
La coppia di stati 1-6 risultano indistinguibili al primo passo. Passiamo alla seconda colonna. Gli stati 2-1 sono già stati verificati, le celle sulla diagonale corrispondono allo stesso stato per cui non vanno verificate, e si passa dunque alla coppia 2-3. Danno valori diversi in uscita per cui segniamo e celle 2-3 e 3-2
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
|
X |
|
|
X |
|
|
2 |
X |
|
X |
|
|
|
|
3 |
|
X |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
X |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
Procedendo nello stesso modo verifichiamo tutte le coppie possibili ottenendo il seguente risultato finale
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
|
X |
|
|
X |
|
|
2 |
X |
|
X |
X |
|
X |
|
3 |
|
X |
|
|
X |
|
|
4 |
|
X |
|
|
X |
|
|
5 |
X |
|
X |
X |
|
X |
|
6 |
|
X |
|
|
X |
|
La tabella ci dice ora quali sono gli stati che si possono distinguere in un solo passo. Passiamo ora a vedere quali stati si possono distinguere in due passi. Per procedere si ragiona nel modo seguente. Gli stati 1 e 3 on sono distinguibili poiché la cella corrispondente alla coppia risulta vuota, vediamo però in quali stati si passa a partire dallo stato 1 e dallo stato 3. applicando l’ingresso a leggiamo dalla tabella di transizione degli stati che da 1 si passa allo stato 3 e dallo stato 3 si passa allo stesso stato 3. quindi, applicando l’ingresso a non potremmo distinguere i due stati perché , se si finisce nello stesso stato, al secondo passo avremo per forza la stessa uscita. Se applichiamo l’ingresso b dallo stato 1 si passa allo stato 2 e dallo stato 3 si passa allo stato 5. Se diamo un’occhiata alla tabella di equivalenza, notiamo che gli stati 2 e 5 sono indistinguibili in un passo, ciò significa che gli stati 1 e 3 sono indistinguibili in due passi poiché al primo passo danno le stesse uscite e poi si transita in stati che sono indistinguibili in un passo, perciò non bastano sequenze di due ingressi per notare differenze di comportamento a partire dagli stati 1 e 3.
Consideriamo ora gli stati 1 e 4. Con l’ingresso a si va rispettivamente negli stati 3 e 5. ma gli stati 3 e 5 sono distinguibili (analizzando la tabella di equivalenza). Ciò significa che 1 e 4 sono indistinguibili in un solo passo, ma sono distinguibili in due passi poiché, dal secondo ingresso cominceremo già a verificare uscite diverse. Contrassegniamo allora le celle 1-4 e 4-1.
Con ragionamento analogo notiamo che gli stati2-5 non sono distinguibili in due passi, poiché con l’ingresso a si va sempre nello stato 2, mentre con l’ingresso b si va rispettivamente negli stati 3 ed 1 che sono indistinguibili.
La coppia 3-4 è distinguibile in due passi poiché già con l’ingresso a si va negli stati 3 e 5 che sono fra loro distinguibili.
Completando la scansione della tabella si ha il risultato finale seguente
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
|
X |
|
X |
X |
|
|
2 |
X |
|
X |
X |
|
X |
|
3 |
|
X |
|
X |
X |
|
|
4 |
X |
X |
X |
|
X |
X |
|
5 |
X |
|
X |
X |
|
X |
|
6 |
|
X |
|
X |
X |
|
Ora la tabella ci dice quali sono gli stati che possiamo sicuramente distinguere in uno o due passi. Raggruppiamo insieme gli stati che non siamo riusciti a distinguere
Creiamo allora i nuovi stati
S1
= {1,3,6}
S2
= {2,5}
S3
= {4}
Costruiamo le tabelle corrispondenti al nuovo automa
|
VI |
a |
b |
|
VI |
a |
b |
|
S1 |
S1 |
S2 |
|
S1 |
0 |
0 |
|
S2 |
S2 |
S1 |
|
S2 |
1 |
1 |
|
S3 |
S2 |
S1 |
|
S3 |
0 |
0 |
Non sappiamo, però, se il nostro sistema è in forma minima o si possano ancora avere semplificazioni. Per verificare dobbiamo costruire una nova tabella di equivalenza riapplicando i metodi visti precedentemente
|
|
1 |
2 |
3 |
|
1 |
|
X |
X |
|
2 |
X |
|
X |
|
3 |
X |
X |
|
Riusciamo a riempire di X tutta la tabella di equivalenza. Ciò significa che il nostro automa semplificato possiede stati che sono tutti distinguibili fra di oro. Abbiamo ottenuto quindi l’automa in forma minima. In caso contrario avremmo dovuto procedere a raggruppare gli stati fra loro indistinguibili, costruire il nuovo automa, costruire la nuova tabella di equivalenza e così vi. Il procedimento di minimizzazione termina quando otteniamo una tabella di equivalenza in cui riempiamo a riempire tutte le caselle (esclusa la diagonale naturalmente).