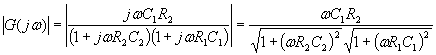Documento word

Documento word zippato

Documento PDF

Amplificatore passabanda invertente

Un amplificatore passabanda ha un’organizzazione circuitale di principio schematizzata nella figura seguente.

       

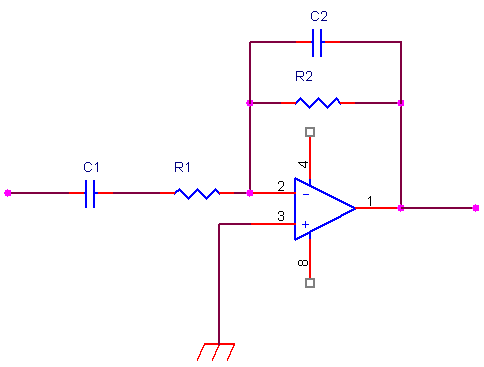
Il circuito è una sorta di fusione di un circuito derivatore ed un circuito integratore. In effetti la risposta in frequenza del amplificatore passabanda, rappresentata nella figura seguente. Il documento allegato mostra i dettagli della risposta in frequenza del dispositivo. Potete scaricare il foglio excel per provare a sperimentare diversi valori dei dispositivi.

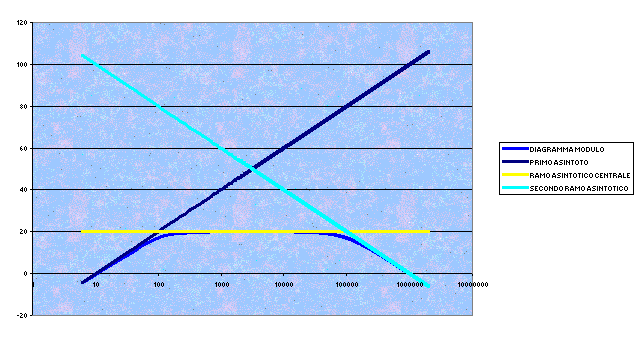è la fusione della prima parte del diagramma della risposta di un derivatore reale e della seconda parte della risposta di un integratore reale. Abbiamo una frequenza di taglio inferiore data dalla formula

e una frequenza di taglio superiore data dalla formula

Per dimostrare il comportamento di questo dispositivo adottiamo dapprima un metodo intuitivo. Dobbiamo dire anzitutto che i due condensatori devono avere valori diversi, con C1 molto più grande di C2. Ricordando che la reattanza capacitiva dipende dall’inverso della capacità

possiamo notare che, in corrispondenza della stessa frequenza, i due condensatori hanno un comportamento molto diverso. IL documento allegato mostra come a basse frequenze, i due condensatori offrono entrambi reattanze molto elevate tanto da poter essere considerati entrambi circuiti aperti. A frequenze più alte il condensatore C2 offre una reattanza molto elevata tanto da poter essere considerato un circuito aperto, mentre il condensatore C1 offre una reattanza molto più bassa per cui può essere considerato un cortocircuito. A frequenze molto più alte i condensatori sono entrambi cortocircuiti. Nel nostro esempio C1 è pari ad 1 microfarad mentre C2 è pari a 10 nanofarad, cioè ha una capacità cento volte più piccola. Alla frequenza di 0,1 Hz la reattanza di C1 è pari a circa 1,6 megaohm mentre la reattanza di C2 è pari a  160 megaohm. A circa 70 Hz il condensatore C1 offre una reattanza di circa 2 kiloohm mentre C2 offre una reattanza di 200 Kilohm. A circa 500 Hz il primo condensaote offre una reattanza di soli 500 ohm mentre il secondo condensatore offre ancora una reattanza di 50 kilohm. A 27 Khz le reattanze sono rispettivamente di 5 ohm e 500 ohm.

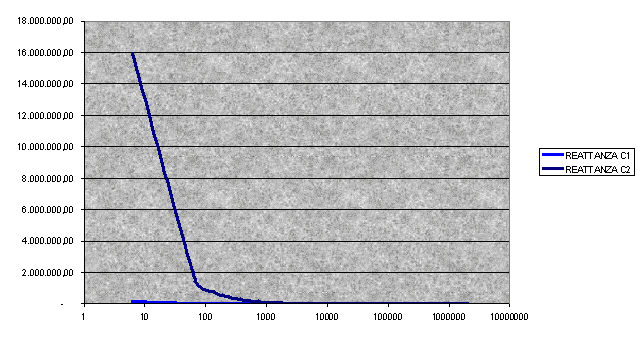
Usando il foglio excel potete divertirvi a sperimentare valori diversi di capacità.

Tutto questo ci consente di dire che a frequenze molto basse, il condensatore C1 blocca il segnale impedendogli di “attraversare” il circuito ed abbiamo un’attenuazione. Al crescere della frequenza la reattanza del condensatore C1 scende mentre la reattanza del secondo condensatore è ancora tanto elevata da poter essere considerato un circuito aperto, per cui il nostro amplificatore si può schematizzare nel modo seguente

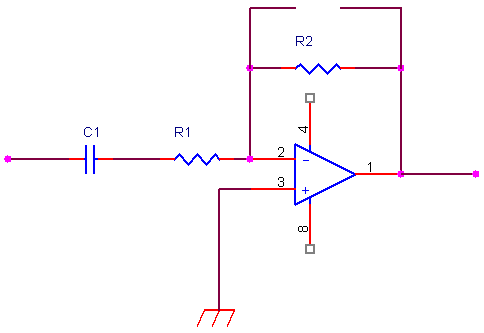
ma questo non è altro che un derivatore ideale, da cui il comportamento mostrato alla prima parte del diagramma.

All’aumentare della frequenza il condensatore C1 è ormai un cortocircuito mentre il condensatore C2 è ancora un circuito aperto

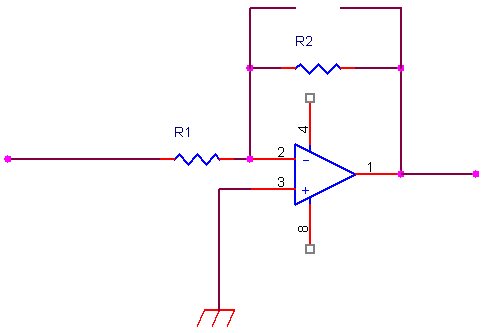
a queste frequenze il dispositivo è diventato un semplice amplificatore in configurazione invertente, con un’amplificazione pari al rapporto fra R2 ed R1 (tratto costante del diagramma della risposta).

Al crescere della frequenza il condensatore C2 non può essere considerato ancora un circuito aperto

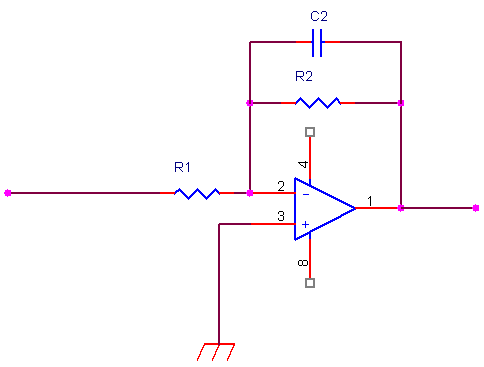
siamo di fronte ad un integratore reale (ultimo tratto del diagramma).

Passiamo ora ad un approccio analitico

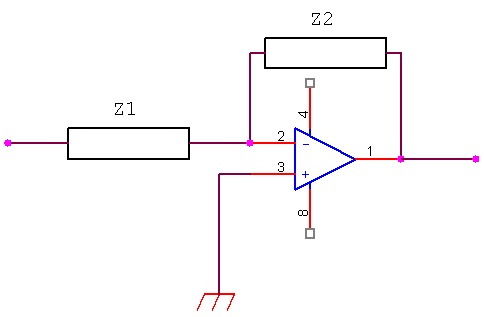
Il parallelo fra C2 ed R2 costituisce l’impedenza Z2 la cui espressione è

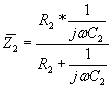
mentre la serie fra R1 e C1 è pari a

La risposta complessiva del sistema è data da

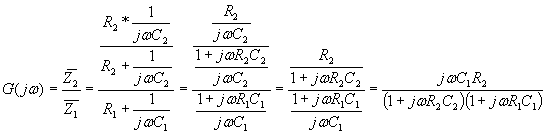
Se consideriamo il modulo della risposta abbiamo

[1]

Il diagramma di tale risposta è ricavato nel documento allegato. Possiamo tracciare un diagramma asintotico: infatti per  si ha che  e  per cui  e quindi, nel suo tratto iniziale, il diagramma della risposta armonica coincide con quello del derivatore ideale. A frequenze intermedie  ma si ha già  per cui 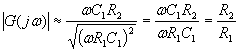 e abbiamo l’asintoto orizzontale. In particolare, per  si ha

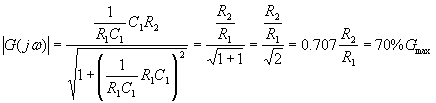
Per cui è dimostrato che esso costituisce la pulsazione di taglio inferiore. A frequenze elevate si ha per cui  e si ha il secondo diagramma asintotico. Per  si ha

 

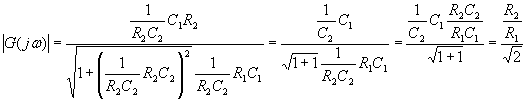
per cui è dimostrato che quello è il valore della frequenza di taglio superiore.

 


[1] Ricordiamo che il modulo del numero complesso a+jb è pari a  e che il modulo del rapporto di due numeri complessi è pari al rapporto dei moduli mentre il modulo del prodotto di due numeri complessi è pari al prodotto dei moduli.