Risposta in frequenza dell’integratore ideale
Filtri attivi (seconda parte)
L’integratore ideale
Consideriamo il seguente circuito
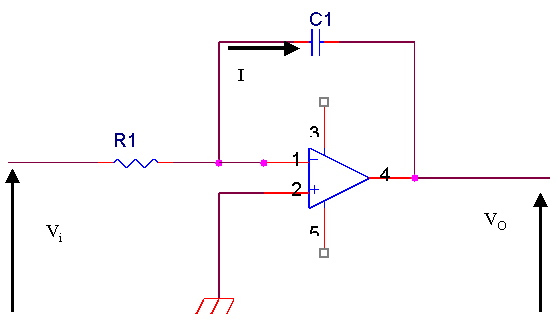
Cerchiamo al solito di ricavare il legame ingresso-uscita. In questa operazione adesso sarete bravissimi, grazie alle vostre
Immense
Divine
Incredibili
Erculee
Inossidabili
Immarcescibili
Pindariche
capacità intellettuali. Al solito, la tensione di uscita, grazie alla massa virtuale (concetto che non ripeto per non offendervi), è la tensione che si trova ai capi del condensatore, per cui
(il segno meno è sempre dovuto al mancato rispetto della convenzione dell’utilizzatore) ma sappiamo che la corrente è la medesima anche nella resistenza R, a causa della resistenza di ingresso infinita dell’operazionale, per cui
A meno di una costante stavolta è la tensione di ingresso che è la derivata della tensione di uscita.
Le vostre potentissime menti logico-matematiche, si staranno chiedendo; ma se la tensione di ingresso è la derivata della tensione di uscita, come si esprime il legame fra tensione di uscita e tensione di ingresso? Dovete ora impadronirvi di un concetto matematico detto integrale (leggete il documento collegato e poi tornate indietro).
Ora che avete fatto un passo da gigante negli universi matematici possiamo dire che
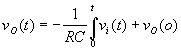
se all’istante zero il condensatore è scarico
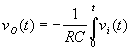
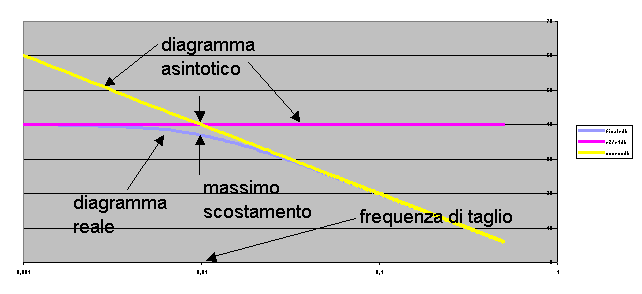
Risposta in frequenza dell’integratore ideale
Per calcolare la risposta in frequenza del circuito procediamo come al solito
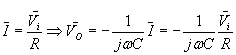
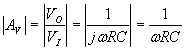
Vediamo già che (sempre sfruttando le vostre inenarrabili capacità mentali) la amplificazione che abbiamo diventa tanto più grande quanto più diminuisce la frequenza, fino a tendere ad infinito. Se passiamo ai decibel abbiamo
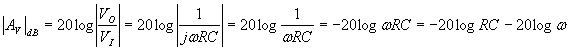
nel diagramma di Bode rappresenta una retta con pendenza negativa di 20 decibel per decade
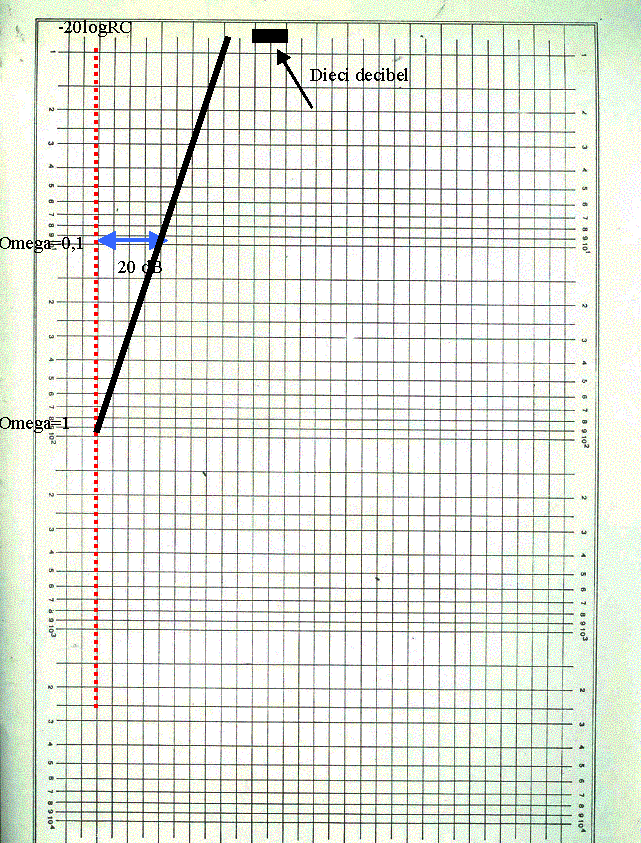
anche in questo caso abbiamo che il circuito si comporta in maniera non corretta perché amplifica troppo il rumore alle bassissime frequenze. Dobbiamo fare in modo da limitare l’amplificazione a bassa frequenza, ottenendo una risposta di questo tipo
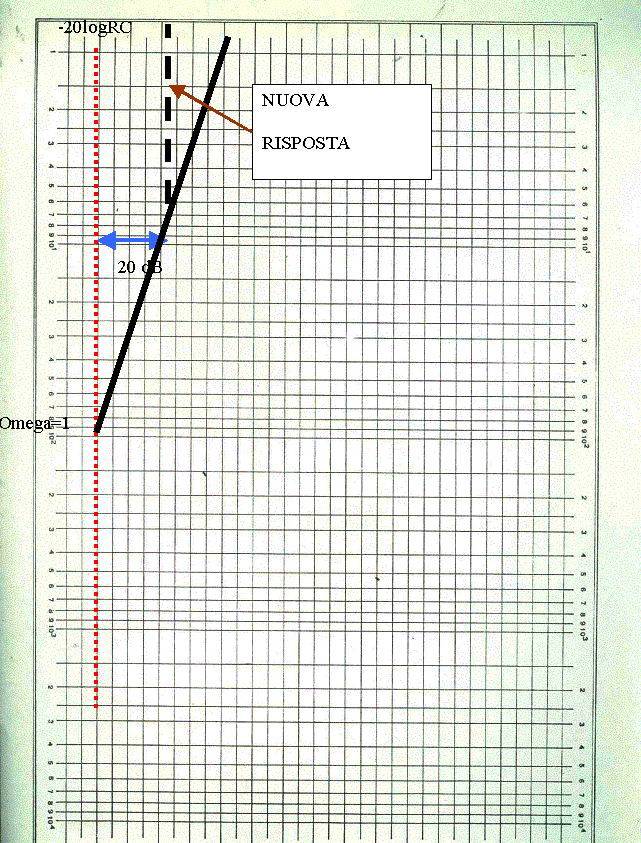
per ottenere tale risposta dobbiamo modificare il circuito.
L’integratore reale
Il circuito è il seguente
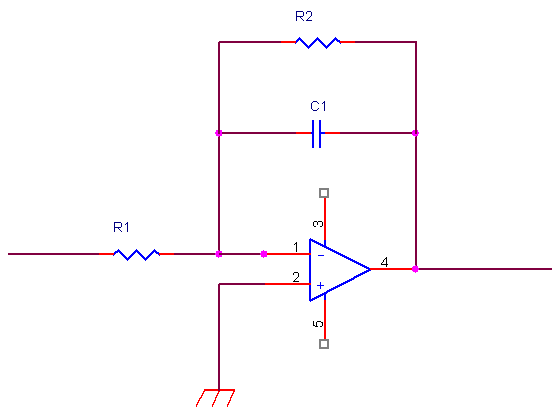
la risposta in frequenza è data dal rapporto fra l’impedenza (costituita dal parallelo fra condensatore ed R2 ) e la resistenza R1
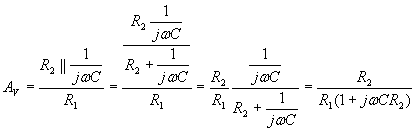
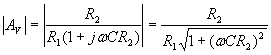
se 
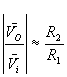e il circuito si
comporta a basse frequenze come un normale amplificatore
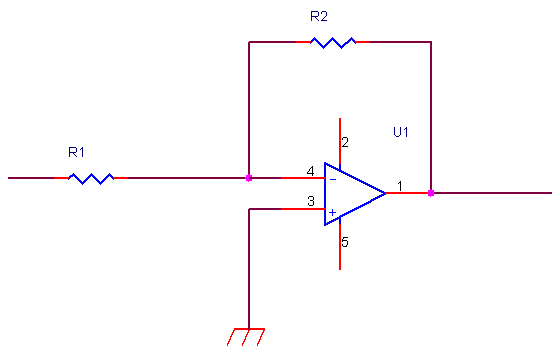
se vogliamo, a basse frequenze il condensatore diventa un
circuito aperto e il parallelo si riduce alla sola resistenza R2.
Vediamo ora cosa accade alle alte frequenze. In questo caso 
per cui
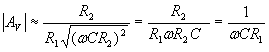
che è la funzione di risposta dell’integratore ideale. Anche in questo caso, a frequenze intermedie, la risposta si discosta dal comportamento asintotico e si può individuare una frequenza di taglio, in corrispondenza della quale si ha il massimo scostamento dal diagramma asintotico, scostamento pari a 3 dB, cioè il 70% dell’amplificazione massima.
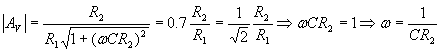
nel foglio excel potete divertirvi a variare i valori delle resistenze e capacità e notare come cambiano i diagrammi asintotici e quello reale
