Documento zippato
Il concetto di derivata
Poiché siete tutti matematici che rivaleggiano con le più grandi menti che hanno calpestato, questo pianeta suppongo che abbiate una qualche frequentazione con il concetto di funzione. Diciamo banalmente che la funzione lega un insieme di valori x ad un insieme di valori y. Un esempio potrebbe essere lo studio dello spazio percorso da un corpo: diligentemente raccogliamo in una tabella gli istanti di tempo in cui facciamo le rilevazioni e in corrispondenza di essi lo spazio percorso.
Tabella 1
|
tempo |
SPAZIO PERCORSO |
|
1 |
0 |
|
1,01 |
0,004321374 |
|
1,02 |
0,008600172 |
|
1,03 |
0,012837225 |
|
1,04 |
0,017033339 |
|
1,05 |
0,021189299 |
|
1,06 |
0,025305865 |
|
1,07 |
0,029383778 |
|
1,08 |
0,033423755 |
|
1,09 |
0,037426498 |
|
1,1 |
0,041392685 |
Otteniamo anche un diagramma riportando su un sistema di assi cartesiani i punti che corrispondono a queste coppie di valori
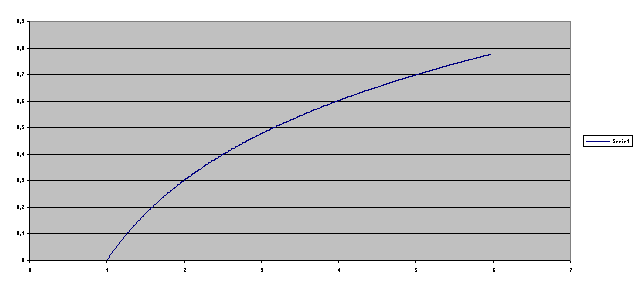
Abbiamo ottenuto il grafico della funzione che lega i valori
degli istanti di tempo (x) con lo spazio percorso (y). A un certo punto ci vien
voglia di studiare la velocità con cui si muove il corpo nei vari intervalli di
tempo. Poiché conosciamo tutti la teoria della relatività generale sappiamo che
se un corpo, in un intervallo di tempo ![]() percorre uno spazio
percorre uno spazio ![]() , si è mosso con una velocità
, si è mosso con una velocità ![]() . Possiamo allora dividere l’intervallo di tempo di
osservazione in tanti intervallini di ampiezza
. Possiamo allora dividere l’intervallo di tempo di
osservazione in tanti intervallini di ampiezza ![]() e misurare lo spazio percorso in tali intervalli. Se
diagrammiamo i risultati otteniamo il seguente grafico delle velocità medie.
e misurare lo spazio percorso in tali intervalli. Se
diagrammiamo i risultati otteniamo il seguente grafico delle velocità medie.
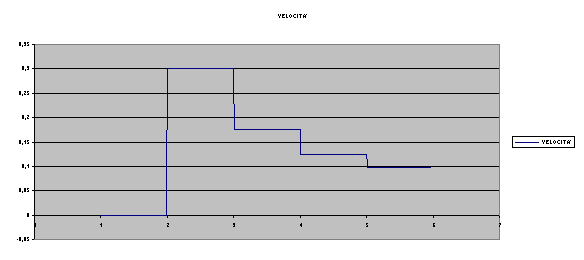
se non siamo soddisfatti della precisione, non ci resta che considerare intervalli di tempo più piccoli
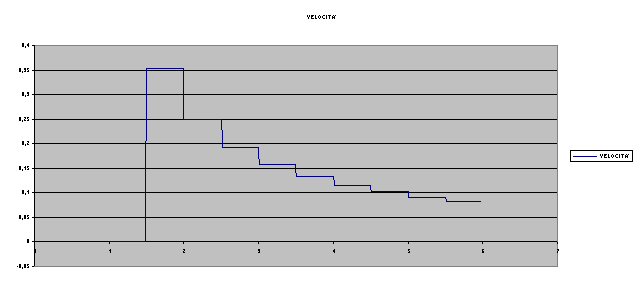
e così via
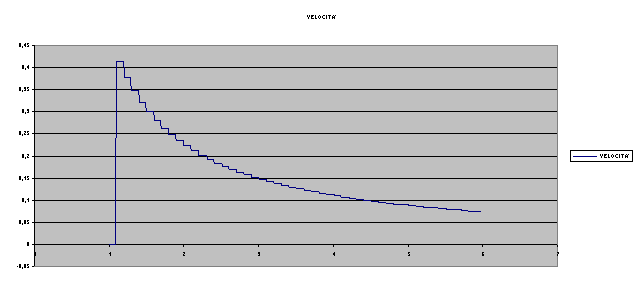
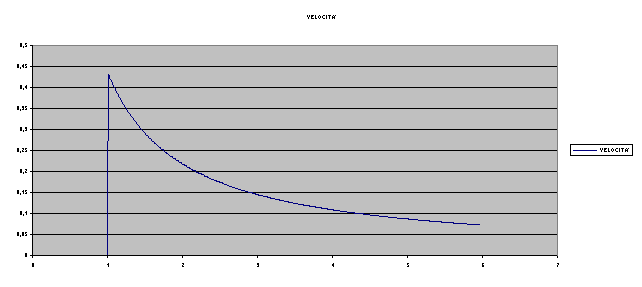
E’ intuitivo che, se facciamo tendere ![]() a zero, otteniamo una
velocità istantanea, cioè una funzione che, istante per istante ci dice la
velocità del nostro copro. Questo è il concetto di derivata in soldini. Data
una funzione f(x), suddividiamo dapprima l’intervallo di variazione della
variabile indipendente x in tanti intervalli
a zero, otteniamo una
velocità istantanea, cioè una funzione che, istante per istante ci dice la
velocità del nostro copro. Questo è il concetto di derivata in soldini. Data
una funzione f(x), suddividiamo dapprima l’intervallo di variazione della
variabile indipendente x in tanti intervalli ![]() . In ogn’uno di questi intervalli calcoliamo l’incremento
della funzione
. In ogn’uno di questi intervalli calcoliamo l’incremento
della funzione ![]() . Costruiamo poi una funzione che, punto per punto, ci da il
rapporto
. Costruiamo poi una funzione che, punto per punto, ci da il
rapporto ![]() detto rapporto
incrementale e quindi ci da la velocità media di variazione della funzione
in questi intervalli. Poi facciamo tendere a zero l’ampiezza degli
intervalli
detto rapporto
incrementale e quindi ci da la velocità media di variazione della funzione
in questi intervalli. Poi facciamo tendere a zero l’ampiezza degli
intervalli ![]() ,. Per voi che avete meritato il Nobel per i vostri studi sui
limiti, non è una sorpresa una simbologia del genere
,. Per voi che avete meritato il Nobel per i vostri studi sui
limiti, non è una sorpresa una simbologia del genere ![]() . Otteniamo una funzione nuova che, punto per punto, ci da la
velocità istantanea di variazione della funzione di partenza. La funzione che
abbiamo ottenuto è detta derivata della funzione di partenza f(x) e si può
indicare in diversi modi diversi: f ’(x),
. Otteniamo una funzione nuova che, punto per punto, ci da la
velocità istantanea di variazione della funzione di partenza. La funzione che
abbiamo ottenuto è detta derivata della funzione di partenza f(x) e si può
indicare in diversi modi diversi: f ’(x), ![]() , Df(x).
, Df(x).
Di seguito mostriamo alcuni esempi di funzioni e loro derivate
|
Funzione |
Derivata |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Farete ulteriori stratosferici passi avanti su questi concetti con la vostra bellissima docente di matematica.